题目内容
 如图,在直线y=-x+3上取一点P,作PA⊥x轴,PB⊥y轴,垂足分别为A、B,若矩形OAPB的面积为4,则这样的点P的坐标是________.
如图,在直线y=-x+3上取一点P,作PA⊥x轴,PB⊥y轴,垂足分别为A、B,若矩形OAPB的面积为4,则这样的点P的坐标是________.
(4,-1),(-1,4)
分析:设点P的坐标,然后根据矩形面积公式得到二元二次方程组,解方程组计算求出点P的坐标.
解答:设点P的坐标为(a,b),由题意得方程组:
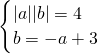
解方程组得:
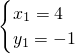
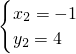
∴点P的坐标为(4,-1),(-1,4).
故答案为:(4,-1),(-1,4).
点评:本题考查的是一次函数的综合题,利用一次函数的性质,结合矩形的面积公式得到方程组求出点P的坐标.
分析:设点P的坐标,然后根据矩形面积公式得到二元二次方程组,解方程组计算求出点P的坐标.
解答:设点P的坐标为(a,b),由题意得方程组:
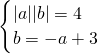
解方程组得:
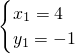
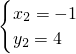
∴点P的坐标为(4,-1),(-1,4).
故答案为:(4,-1),(-1,4).
点评:本题考查的是一次函数的综合题,利用一次函数的性质,结合矩形的面积公式得到方程组求出点P的坐标.

练习册系列答案
相关题目
如图,在直线上任取1个点,2个点,3个点,4个点,
(1)填写下表:
(2)在直线上取n个点,可以得到几条射线?
(3)用这种方法可以得到15条线段吗?如果可以,请指出取几个点;不能,请说明理由.

(1)填写下表:
| 点的个数 | 所得线段的条数 | 所得射线的条数 |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
(3)用这种方法可以得到15条线段吗?如果可以,请指出取几个点;不能,请说明理由.


 13、如图,在直线L上顺次排列着5个点,即点A,B,C,D,E,则5个点中到其余各点的距离之和最小的点是( )
13、如图,在直线L上顺次排列着5个点,即点A,B,C,D,E,则5个点中到其余各点的距离之和最小的点是( )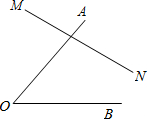 已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)
已知:如图,在直线MN上求作一点P,使点P到∠AOB两边的距离相等(要求写出作法,并保留作图痕迹,写出结论)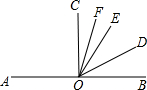 如图,在直线AB上取一点O,在AB同侧引射线OC、OD、OE、OF,使∠COE和∠BOE互余,射线OF和OD分别平分∠COE和∠BOE.试探究∠AOF+∠BOD与∠DOF的关系,并说明理由.
如图,在直线AB上取一点O,在AB同侧引射线OC、OD、OE、OF,使∠COE和∠BOE互余,射线OF和OD分别平分∠COE和∠BOE.试探究∠AOF+∠BOD与∠DOF的关系,并说明理由.