��Ŀ����
��ͼ��������y=ax2+bx+2��x����A��﹣1��0����B��4��0�����㣬��y���ڵ�C�������C��ƽ����x���ֱ�߽�����һ��D����P����������һ���㣮

��1���������߽���ʽ����D���ꣻ
��2����E��x���ϣ�����A��E��D��PΪ������ı�����ƽ���ı��Σ����ʱ��P�����ꣻ
��3������P��ֱ��CD�Ĵ��ߣ�����ΪQ��������CPQ��CP���ۣ���Q�Ķ�Ӧ��ΪQ�䣮�Ƿ���ڵ�P��ʹQ��ǡ������x���ϣ������ڣ������ʱ��P�����ꣻ�������ڣ�˵�����ɣ�
��![]() ��
��
��ã�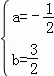
��y=﹣![]() x2+
x2+![]() x+2��
x+2��
��y=2ʱ��﹣![]() x2+
x2+![]() x+2=2����ã�x1=3��x2=0���ᣩ��
x+2=2����ã�x1=3��x2=0���ᣩ��
������D������3��2����
��2��A��E���㶼��x���ϣ�AE�����ֿ��ܣ�
�ٵ�AEΪһ��ʱ��AE��PD��
��P1��0��2����
�ڵ�AEΪ�Խ���ʱ������ƽ���ı��ζԶ��㵽��һ���Խ��߾�����ȣ�
��֪P�㡢D�㵽ֱ��AE����x�ᣩ�ľ�����ȣ�
��P���������Ϊ﹣2��
���������ߵĽ���ʽ��﹣![]() x2+
x2+![]() x+2=﹣2
x+2=﹣2
��ã�x1=![]() ��x2=
��x2=![]() ��
��
��P�������Ϊ��![]() ��﹣2������
��﹣2������![]() ��﹣2��
��﹣2��
����������P1��0��2����P2��![]() ��﹣2����P3��
��﹣2����P3��![]() ��﹣2����
��﹣2����
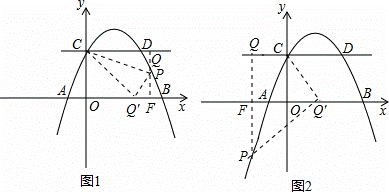
��3���������������ĵ�P����Ȼ��P��ֱ��CD�·�����ֱ��PQ��x����F����P������Ϊ��a��﹣![]() a2+
a2+![]() a+2����
a+2����
�ٵ�P����y���Ҳ�ʱ����ͼ1����CQ=a��
PQ=2﹣��﹣![]() a2+
a2+![]() a+2��=
a+2��=![]() a2﹣
a2﹣![]() a��
a��
�֡ߡ�CQ��O+��FQ��P=90�㣬��COQ��=��Q��FP=90�㣬
���FQ��P=��OCQ�䣬
���COQ��ס�Q��FP��![]() ��
��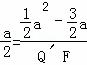 ��
��
��Q��F=a﹣3��
��OQ��=OF﹣Q��F=a﹣��a﹣3��=3��CQ=CQ��=![]() =
=![]() ��
��
��ʱa=![]() ����P������Ϊ��
����P��������![]() ��
��![]() ����
����
�ڵ�P����y�����ʱ����ͼ2����ʱa��0��﹣![]() a2+
a2+![]() a+2��0��CQ=﹣a��
a+2��0��CQ=﹣a��
PQ=2﹣��﹣![]() a2+
a2+![]() a+2��=
a+2��=![]() a2﹣
a2﹣![]() a��
a��
�֡ߡ�CQ��O+��FQ��P=90�㣬��CQ��O+��OCQ��=90�㣬
���FQ��P=��OCQ�䣬��COQ��=��Q��FP=90�㣬
���COQ��ס�Q��FP��![]() ��
��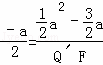 ��Q��F=3﹣a��
��Q��F=3﹣a��
��OQ��=3��
CQ=CQ��=![]() =
=![]() ��
��
��ʱa=﹣![]() ����P������Ϊ��﹣
����P������Ϊ��﹣![]() ��
��![]() ����
����
�������������������ĵ�P����Ϊ��![]() ��
��![]() ������﹣
������﹣![]() ��
��![]() ����
����

 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д� ���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣�
���㣬���ʵ�xΪ��ֵʱ���߶�CD�����ֵ�������ֵΪ���٣� OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1��
OΪ����ԭ�㣬��������һ��C�ĺ�����Ϊ1�� ���������ϣ��������Ϊ12��
���������ϣ��������Ϊ12�� ��x�ύ�ڵ�A��B����A������Ϊ��-2��0����
��x�ύ�ڵ�A��B����A������Ϊ��-2��0����