ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ![]() ÷–Θ§
÷–Θ§![]() =5Θ§
=5Θ§![]() =9Θ§
=9Θ§![]() =
=![]() Θ§Ε·Βψ
Θ§Ε·Βψ![]() ¥”
¥”![]() ≥ωΖΔΘ§―Ί…δœΏ
≥ωΖΔΘ§―Ί…δœΏ![]() ΖΫœρ“‘ΟΩΟκ5ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ε·Βψ
ΖΫœρ“‘ΟΩΟκ5ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»‘ΥΕ·Θ§Ε·Βψ![]() ¥”
¥”![]() Βψ≥ωΖΔΘ§“ΜœύΆ§ΒΡΥΌΕ»‘ΎœΏΕΈ
Βψ≥ωΖΔΘ§“ΜœύΆ§ΒΡΥΌΕ»‘ΎœΏΕΈ![]() …œ”…
…œ”…![]() œρ
œρ![]() ‘ΥΕ·Θ§Β±
‘ΥΕ·Θ§Β±![]() Βψ‘ΥΕ·ΒΫ
Βψ‘ΥΕ·ΒΫ![]() Βψ ±Θ§
Βψ ±Θ§![]() ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§“‘
ΝΫΒψΆ§ ±ΆΘ÷Ι‘ΥΕ·Θ§“‘![]() ΈΣ±ΏΉς’ΐΖΫ–Έ
ΈΣ±ΏΉς’ΐΖΫ–Έ![]() (
(![]() Α¥Ρφ ±’κ≈≈–ρ)Θ§“‘
Α¥Ρφ ±’κ≈≈–ρ)Θ§“‘![]() ΈΣ±Ώ‘Ύ
ΈΣ±Ώ‘Ύ![]() …œΖΫΉς’ΐΖΫ–Έ
…œΖΫΉς’ΐΖΫ–Έ![]() .
.
(1)![]() _______.
_______.
(2)…ηΒψ![]() ‘ΥΕ· ±ΦδΈΣ
‘ΥΕ· ±ΦδΈΣ![]() Θ§’ΐΖΫ–Έ
Θ§’ΐΖΫ–Έ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() ,«κΧΫΨΩ
,«κΧΫΨΩ![]() «Ζώ¥φ‘ΎΉν–Γ÷ΒΘΩ»τ¥φ‘ΎΘ§«σ≥ω’βΗωΉν–Γ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
«Ζώ¥φ‘ΎΉν–Γ÷ΒΘΩ»τ¥φ‘ΎΘ§«σ≥ω’βΗωΉν–Γ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”….
(3)Β±![]() ΈΣΚΈ÷Β ±Θ§’ΐΖΫ–Έ
ΈΣΚΈ÷Β ±Θ§’ΐΖΫ–Έ![]() ΒΡΡ≥ΗωΕΞΒψ(
ΒΡΡ≥ΗωΕΞΒψ(![]() Βψ≥ΐΆβ)¬δ‘Ύ’ΐΖΫ–Έ
Βψ≥ΐΆβ)¬δ‘Ύ’ΐΖΫ–Έ![]() ΒΡ±Ώ
ΒΡ±Ώ![]() …œΘ§«κ÷±Ϋ”–¥≥ω
…œΘ§«κ÷±Ϋ”–¥≥ω![]() ΒΡ÷Β.
ΒΡ÷Β.
ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)¥φ‘ΎΘ§
ΘΜ(2)¥φ‘ΎΘ§![]() ΘΜ(3)
ΘΜ(3)![]() Μρ
Μρ![]() .
.
ΓΨΫβΈωΓΩ
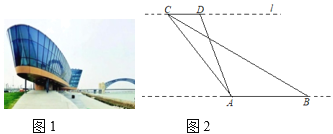
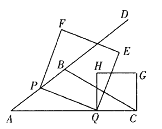
(1)ΙΐΒψBΉςBMΓΆAC”ΎΒψM.ΗυΨί»ΐΫ«–ΈΒΡΟφΜΐΙΪ ΫΘ§«σΒΟ![]() .”…Ι¥Ι…Ε®άμΒΟ
.”…Ι¥Ι…Ε®άμΒΟ![]() Θ§¥”ΕχΒΟΒΫ
Θ§¥”ΕχΒΟΒΫ![]() .
.
(2)¥φ‘Ύ.ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψN.”…Χβ“βΩ…ΒΟ
”ΎΒψN.”…Χβ“βΩ…ΒΟ![]() ,“ρΈΣ
,“ρΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() .ΒΟΒΫ
.ΒΟΒΫ![]() .ΗυΨίΙ¥Ι…Ε®άμΒΟ
.ΗυΨίΙ¥Ι…Ε®άμΒΟ![]() ,‘ρ
,‘ρ
![]() Θ§‘ΌΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ϋχ––«σΫβΦ¥Ω…ΒΟΒΫ¥πΑΗ.
Θ§‘ΌΗυΨίΕΰ¥ΈΚ· ΐΒΡ–‘÷ Ϋχ––«σΫβΦ¥Ω…ΒΟΒΫ¥πΑΗ.
ΫβΘΚ(1)ΙΐΒψBΉςBMΓΆAC”ΎΒψM.
![]() Θ§
Θ§
![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
ΫβΒΟ![]() .
.
”…Ι¥Ι…Ε®άμΘ§ΒΟ![]() Θ§
Θ§
‘ρ![]() .
.
(2)¥φ‘Ύ.
ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψN.“άΧβ“βΒΟ
”ΎΒψN.“άΧβ“βΒΟ![]() ,
,
![]() Θ§
Θ§
![]() .
.
![]() .
.
ΗυΨίΙ¥Ι…Ε®άμΒΟ![]() ,
,
![]() (
(![]() ).
).
![]() ,
,![]() .
.
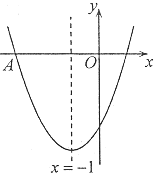
ΔΌ»γΆΦ1Θ§Β±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œ ±Θ§
…œ ±Θ§![]() ΘΜ
ΘΜ
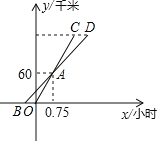
ΔΎ»γΆΦ2Θ§Β±Βψ![]() ‘Ύ±Ώ
‘Ύ±Ώ![]() …œ ±Θ§
…œ ±Θ§![]() .
.


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ