题目内容
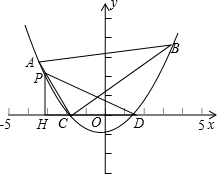 (2012•常德)如图,已知二次函数y=
(2012•常德)如图,已知二次函数y=| 1 | 48 |
(1)求二次函数的解析式:
(2)求证:△ACB是直角三角形;
(3)若点P在第二象限,且是抛物线上的一动点,过点P作PH垂直x轴于点H,是否存在以P、H、D为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
分析:(1)将点A及点B的坐标代入函数解析式,得出a、b的值,继而可得出函数解析式;
(2)根据二次函数解析式,求出点C的坐标,然后分别求出AC、AB、BC的长度,利用勾股定理的逆定理证明即可;
(3)分两种情况进行讨论,①△DHP∽△BCA,②△PHD∽△BCA,然后分别利用相似三角形对应边成比例的性质求出点P的坐标.
(2)根据二次函数解析式,求出点C的坐标,然后分别求出AC、AB、BC的长度,利用勾股定理的逆定理证明即可;
(3)分两种情况进行讨论,①△DHP∽△BCA,②△PHD∽△BCA,然后分别利用相似三角形对应边成比例的性质求出点P的坐标.
解答:解:(1)由题意得,函数图象经过点A(-4,3),B(4,4),
故可得:
,
解得:
,
故二次函数关系式为:y=
(x+2)(13x-20).
(2)由(1)所求函数关系式可得点C坐标为(-2,0),点D坐标为(
,0),
又∵点A(-4,3),B(4,4),
∴AB=
=
,AC=
=
,BC=
=
,
∵满足AB2=AC2+BC2,
∴△ACB是直角三角形.
(3)存在点P的坐标,点P的坐标为(-
,
)或(-
,
).
设点P坐标为(x,
(x+2)(13x-20)),则PH=
(x+2)(13x-20),HD=-x+
,
①若△DHP∽△BCA,则
=
,即
=
,
解得:x=-
或x=
(因为点P在第二象限,故舍去);
代入可得PH=
,即P1坐标为(-
,
);
②若△PHD∽△BCA,则
=
,即
=
,
解得:x=-
或x=
(因为点P在第二象限,故舍去).
代入可得PH=
,即P2坐标为:(-
,
).
综上所述,满足条件的点P有两个,即P1(-
,
)、P2(-
,
).
故可得:
|
解得:
|
故二次函数关系式为:y=
| 1 |
| 48 |
(2)由(1)所求函数关系式可得点C坐标为(-2,0),点D坐标为(
| 20 |
| 13 |
又∵点A(-4,3),B(4,4),
∴AB=
| (4+4)2+(4-3)2 |
| 65 |
| (-2+4)2+(0-3)2 |
| 13 |
| (4+2)2+(4-0)2 |
| 52 |
∵满足AB2=AC2+BC2,
∴△ACB是直角三角形.
(3)存在点P的坐标,点P的坐标为(-
| 50 |
| 13 |
| 35 |
| 13 |
| 122 |
| 13 |
| 284 |
| 13 |
设点P坐标为(x,
| 1 |
| 48 |
| 1 |
| 48 |
| 20 |
| 13 |
①若△DHP∽△BCA,则
| PH |
| AC |
| DH |
| BC |
| ||
|
-x+
| ||
|
解得:x=-
| 50 |
| 13 |
| 20 |
| 13 |
代入可得PH=
| 35 |
| 13 |
| 50 |
| 13 |
| 35 |
| 13 |
②若△PHD∽△BCA,则
| PH |
| BC |
| HD |
| AC |
| ||
|
-x+
| ||
|
解得:x=-
| 122 |
| 13 |
| 20 |
| 13 |
代入可得PH=
| 284 |
| 13 |
| 122 |
| 13 |
| 284 |
| 13 |
综上所述,满足条件的点P有两个,即P1(-
| 50 |
| 13 |
| 35 |
| 13 |
| 122 |
| 13 |
| 284 |
| 13 |
点评:此题属于二次函数综合题目,涉及了相似三角形的判定与性质、待定系数法求二次函数解析式,同时还让学生探究存在性问题,本题的第三问计算量比较大,同学们要注意细心求解.

练习册系列答案
相关题目
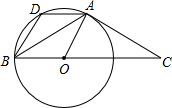 (2012•常德)如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D,
(2012•常德)如图,已知AB=AC,∠BAC=120°,在BC上取一点O,以O为圆心OB为半径作圆,且⊙O过A点,过A作AD∥BC交⊙O于D, (2012•常德)如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DC=2,则D到AB边的距离是
(2012•常德)如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,DC=2,则D到AB边的距离是 (2012•常德)如图所给的三视图表示的几何体是( )
(2012•常德)如图所给的三视图表示的几何体是( )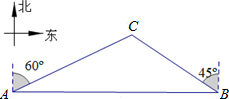 (2012•常德)如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里∕小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船.问我渔政船的航行路程是多少海里?(结果保留根号)
(2012•常德)如图,一天,我国一渔政船航行到A处时,发现正东方向的我领海区域B处有一可疑渔船,正在以12海里∕小时的速度向西北方向航行,我渔政船立即沿北偏东60°方向航行,1.5小时后,在我领海区域的C处截获可疑渔船.问我渔政船的航行路程是多少海里?(结果保留根号)