题目内容
 如图,⊙A与x轴相切,与y轴相交于点B(0,1)、C(0,3),那么扇形BAC的面积是________.
如图,⊙A与x轴相切,与y轴相交于点B(0,1)、C(0,3),那么扇形BAC的面积是________.

分析:利用垂径定理的内容得出BF=CF,进而得出AD与半径的关系,从而得出△ABC为等边三角形,利用扇形面积公式求出即可.
解答:
 解:做AF⊥BC,假设⊙A与x轴相切于E点,连接AE,做BD⊥AE,
解:做AF⊥BC,假设⊙A与x轴相切于E点,连接AE,做BD⊥AE,假设AE=x,图象与y轴相交于点B(0,1)、C(0,3),
∴OB=DE=1,AD=X-1,
∵AC=AB,AF⊥BC,
∴BF=CF=1,
∴AD=BF=1=x-1,
解得:x=2,
∴AB=BC=AC=2,
△ABC为等边三角形,
∴∠BAC=60°,
∴扇形BAC的面积是:
 =
= π.
π.故答案为:
 π.
π.点评:此题主要考查了等边三角形的判定方法以及扇形的面积求法等知识,利用已知得出BF=AD是解决问题的关键.

练习册系列答案
相关题目
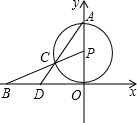 轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.
轴上.连接BP交⊙P于点C,连接AC并延长交x轴于点D.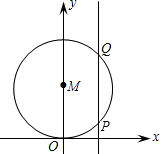 如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标.
如图,⊙M与x轴相切于原点,平行于y轴的直线交圆于P、Q两点,P点在Q点的下方.若P点的坐标是(2,1),求圆心M的坐标. 如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是
如图,⊙M与x轴相切于原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方.若点P的坐标是(2,1),则圆心M的坐标是 (2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是
(2013•仓山区模拟)如图,⊙M与x轴相切与原点,平行于y轴的直线交⊙M于P、Q两点,P点在Q点的下方,若点P的坐标是 (2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(
(2012•黔西南州模拟)如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(