题目内容
某学习小组在探索“各内角都相等的圆内接多边形是否为正多边形”时,进行如下讨论:
甲同学:这种多边形不一定是正多边形,如圆内接矩形;
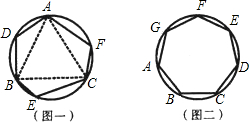
乙同学:我发现边数是6时,它也不一定是正多边形.如图一,△ABC是正三角形,AD=BE=CF,可以证明六边形ADBECF的各内角相等,但它未必是正六边形;
丙同学:我能证明,边数是5时,它是正多边形.我想,边数是7时,它可能也是正多边形.
(1)请你说明乙同学构造的六边形各内角相等.
(2)请你证明,各内角都相等的圆内接七边形ABCDEFG(如图二)是正七边形(不必写已知、求证).
(3)根据以上探索过程,提出你的猜想(不必证明).

答案:
解析:
解析:
|
解:(1)由图知∠AFC对 因为 而∠DAF对的 所以∠AFC=∠DAF. 同理可证,其余各角都等于∠AFC. 所以,图一中六边形各内角相等; (2)因为∠A对 又因为∠A=∠B,所以 所以 同理, 所以七边形ABCDEFG是正七边形; (3)猜想:当边数是奇数时(或当边数是3,5,7,9……时),各内角相等的圆内接多边形是正多边形. |

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

 证)
证)
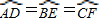 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.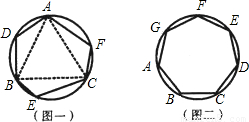
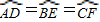 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.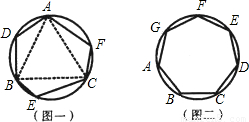
 ,证明六边形ADBECF的各内角相等,但它未必是正六边形.
,证明六边形ADBECF的各内角相等,但它未必是正六边形.