题目内容
(2003•湖州)如图,直线y=kx-2(k>0)与双曲线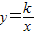 在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .
在第一象限内的交点R,与x轴、y轴的交点分别为P、Q.过R作RM⊥x轴,M为垂足,若△OPQ与△PRM的面积相等,则k的值等于 .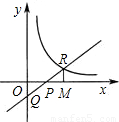
【答案】分析:根据△OPQ与△PRM的面积相等,可以得到两三角形全等,先根据一次函数求出点P、Q的坐标,进而得到OP、OQ的长度,再根据三角形全等表示出点R的坐标,代入反比例函数表达式,解方程即可求得k的值.
解答:解:∵y=kx-2,
∴当x=0时,y=-2,
当y=0时,kx-2=0,解得x= ,
,
所以点P( ,0),点Q(0,-2),
,0),点Q(0,-2),
所以OP= ,OQ=2,
,OQ=2,
∵RM⊥x轴,
∴△OPQ∽△MPR,
∵△OPQ与△PRM的面积相等,
∴△OPQ与△PRM的相似比为1,即△OPQ≌△MPR,
∴OM=2OP= ,RM=OQ=2,
,RM=OQ=2,
所以点R( ,2),
,2),
∵双曲线 经过点R,
经过点R,
∴ =2,即k2=8,
=2,即k2=8,
解得k1=2 ,k2=-2
,k2=-2 (舍去).
(舍去).
故答案为:2 .
.
点评:本题综合考查了一次函数和反比例函数图象的性质,利用三角形面积相等得到两三角形全等是解本题的突破口,也是解题的关键.
解答:解:∵y=kx-2,
∴当x=0时,y=-2,
当y=0时,kx-2=0,解得x=
 ,
,所以点P(
 ,0),点Q(0,-2),
,0),点Q(0,-2),所以OP=
 ,OQ=2,
,OQ=2,∵RM⊥x轴,
∴△OPQ∽△MPR,
∵△OPQ与△PRM的面积相等,
∴△OPQ与△PRM的相似比为1,即△OPQ≌△MPR,
∴OM=2OP=
 ,RM=OQ=2,
,RM=OQ=2,所以点R(
 ,2),
,2),∵双曲线
 经过点R,
经过点R,∴
 =2,即k2=8,
=2,即k2=8,解得k1=2
 ,k2=-2
,k2=-2 (舍去).
(舍去).故答案为:2
 .
.点评:本题综合考查了一次函数和反比例函数图象的性质,利用三角形面积相等得到两三角形全等是解本题的突破口,也是解题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目