题目内容
某机械厂从2009年起每年都投入一定的资金进行技术改造,经技术改造后,其产品的生产成本不断降低,具体数据如表:
| 年度 | 2009 | 2010 | 2011 | 2012 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 每件产品的生产成本y(万元) | 7.2 | 6 | 4.5 | 4 |
(2)该厂计划在2013年把每件产品的生产成本降到3.2万元以下(含3.2万元)如果投入5万元技改资金,是否能满足要求?若不能满足要求,至少还需要再投入多少万元的技改资金(结果精确到0.01万元)?
解:(1)由表中数据知,x、y关系:
xy=2.5×7.2=3×6=4×4.5=4.5×4=18
∴xy=18
∴x、y不是一次函数关系
∴表中数据是反比例函数关系y=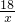 ;
;
(2)当x=5万元时,y=3.6.
4-3.6=0.4(万元),
∴生产成本每件比2009年降低0.4万元.
当y=3.2万元时,3.2=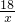 .
.
∴x=5.625
∴5.625-5=0.625≈0.63(万元)
∴还约需投入0.63万元.
分析:(1)根据实际题意和数据特点分情况求解,根据排除法可知其为反比例函数,利用待定系数法求解即可;
(2)直接把x=5万元和y=3.2分别代入函数解析式即可求解.
点评:主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.
xy=2.5×7.2=3×6=4×4.5=4.5×4=18
∴xy=18
∴x、y不是一次函数关系
∴表中数据是反比例函数关系y=
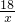 ;
;(2)当x=5万元时,y=3.6.
4-3.6=0.4(万元),
∴生产成本每件比2009年降低0.4万元.
当y=3.2万元时,3.2=
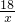 .
.∴x=5.625
∴5.625-5=0.625≈0.63(万元)
∴还约需投入0.63万元.
分析:(1)根据实际题意和数据特点分情况求解,根据排除法可知其为反比例函数,利用待定系数法求解即可;
(2)直接把x=5万元和y=3.2分别代入函数解析式即可求解.
点评:主要考查了函数的实际应用.解题的关键是根据实际意义列出函数关系式,从实际意义中找到对应的变量的值,利用待定系数法求出函数解析式,再根据自变量的值求算对应的函数值.

练习册系列答案
相关题目