Question

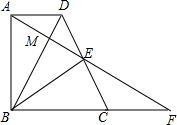如图，在直角梯形ABCD中，AD∥BC，∠DAB=∠ABC=90°，E为CD的中点，联结AE并延长交BC的延长线于F；
（1）联结BE，求证：BE=EF．
（2）联结BD交AE于M，当AD=1，AB=2，AM=EM时，求CD的长．

Answer 1

考点：直角梯形,全等三角形的判定与性质,勾股定理,平行线分线段成比例

专题：

分析：（1）证明△DAE≌△CFE可得AE=FE，再根据直角三角形的性质可得BE=EF；
（2）过D作DH⊥BF于H，证明四边形ABHD为矩形，再由AD=BH，可得AD=CH，进而得到CH=1，然后根据勾股定理可得答案．

解答：（1）证明：∵ABCD为直角梯形，∠A=∠ABC=90°，AD∥BC，
∴∠DAE=∠CFE，∠ADE=∠FCE，
∵E为CD的中点，
∴DE=CE，
在△DAE和△CFE中，

∠DAE=∠F ∠ADE=∠FCE DE=CE

，
∴△DAE≌△CFE（AAS），
∴AE=FE，AD=FC，
在直角三角形ABF中：BE=AE=FE；

（2）∵AM=EM，AE=FE，
∴AM=

1

3

FM，
∵AD∥BC，
∴

AD

BF

=

AM

FM

=

1

3

，
过D作DH⊥BF于H，
∴∠DHB=90°，
∵∠DAB=∠ABC=90°，
∴四边形ABHD为矩形，
∵AD=BH，∴AD=CH，
在直角三角形CDH中，CH=AD=1，DH=AB=2，
CD=

DH2+CH2

=

5

．

点评：此题主要考查了直角梯形，关键是掌握直角梯形中常用辅助线，作高，构造矩形和直角三角形．