题目内容
如图，有一边长为4的等边三角形纸片，要从中剪出三个面积相等的扇形，那么剪下的其中一个扇形ADE（阴影部分）的面积为 ；若用剪下的一个扇形围成一个圆锥，该圆锥的底面圆的半径r是 ．
扇形的面积公式是：S=
，代入公式就可以求出扇形的面积；根据圆锥的侧面积：S侧= 
?2πr?l=πrl代入数据可得答案．
解：∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，
∵要从中剪出三个面积相等的扇形，
∴AD=DB=AB=2，
∴扇形ADE（阴影部分）的面积为：S==
π；
πrl=π，
π×r×2=π，
r=
，
故答案为：π；．
此题主要考查了扇形面积求法以及圆锥侧面展开图的性质，根据已知得出圆锥侧面展开图与圆锥各部分对应情况是解题关键．
，代入公式就可以求出扇形的面积；根据圆锥的侧面积：S侧= ?2πr?l=πrl代入数据可得答案．解：∵△ABC是等边三角形，
∴∠A=∠B=∠C=60°，
∵要从中剪出三个面积相等的扇形，
∴AD=DB=
AB=2，∴扇形ADE（阴影部分）的面积为：S=
=π；πrl=
π，π×r×2=
π，r=
，故答案为：
π；．此题主要考查了扇形面积求法以及圆锥侧面展开图的性质，根据已知得出圆锥侧面展开图与圆锥各部分对应情况是解题关键．
练习册系列答案
相关题目
CAB上一点，若∠ABC=20°，则∠D的度数是______．
、
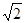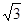，则∠BAC的度数为 _____.
的半径为2cm，⊙
的半径为4cm，圆心距