题目内容
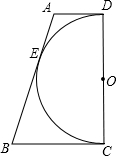如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD，下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形与半圆的面积之比（ ）| A、4：π | B、5：π | C、6：π | D、7：π |
分析：利用切线长定理可知AD=AE，BE=BC，再根据梯形、半圆的面积公式计算即可求出面积比．
解答：解：
∵AD=AE，BE=BC，
∴S梯形=（AD+CB）×4÷2=5×4÷2=10，
∴半圆的面积=
=2π，
∴面积比=5：π．
故选B．
∵AD=AE，BE=BC，
∴S梯形=（AD+CB）×4÷2=5×4÷2=10，
∴半圆的面积=
| π×4 |
| 2 |
∴面积比=5：π．
故选B．
点评：本题主要是利用梯形面积和圆的面积公式求出面积．
练习册系列答案
相关题目
6、如图，已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切，切点分别是D，C，E．若半圆O的半径为2，梯形的腰AB为5，则该梯形的周长是（ ）
