题目内容
已知,关于x的一次函数y=(1-3a)x+2a-4的图象不经过第三象限.
(1)当-2≤x≤5时,______≤y≤______.(用含a的代数式表示)
(2)确定a的取值范围.
解:(1)∵当x=-2时,y=-2(1-3a)+2a-4=8a-6;
∴当x=5时,y=5(1-3a)+2a-4=-13a+1;
∵关于x的一次函数y=(1-3a)x+2a-4的图象不经过第三象限,
∴y的值随x的值增大而减小,
∴当-2≤x≤5时,-13a+1≤y≤8a-6;
(2)关于x的一次函数y=(1-3a)x+2a-4的图象不经过第三象限,即一次函数y=(1-3a)x+2a-4的图象经过一、二、四象限或二、四象限,
∴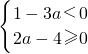 ,
,
∴a≥2.
故答案为-13a+1,8a-6.
分析:(1)先将x=-2与x=5分别代入y=(1-3a)x+2a-4,求出对应的y值,再根据一次函数的性质即可求出y的取值范围;
(2)根据一次函数的图象与系数的关系,当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,列出关于a的不等式组,即可求解.
点评:本题主要考查了一次函数的性质.一次函数y=kx+b的图象经过的象限由k、b的值共同决定,有六种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小;
⑤当k>0,b=0,函数y=kx+b的图象经过第一、三象限;
⑥当k<0,b=0,函数y=kx+b的图象经过第二、四象限.
∴当x=5时,y=5(1-3a)+2a-4=-13a+1;
∵关于x的一次函数y=(1-3a)x+2a-4的图象不经过第三象限,
∴y的值随x的值增大而减小,
∴当-2≤x≤5时,-13a+1≤y≤8a-6;
(2)关于x的一次函数y=(1-3a)x+2a-4的图象不经过第三象限,即一次函数y=(1-3a)x+2a-4的图象经过一、二、四象限或二、四象限,
∴
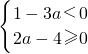 ,
,∴a≥2.
故答案为-13a+1,8a-6.
分析:(1)先将x=-2与x=5分别代入y=(1-3a)x+2a-4,求出对应的y值,再根据一次函数的性质即可求出y的取值范围;
(2)根据一次函数的图象与系数的关系,当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,列出关于a的不等式组,即可求解.
点评:本题主要考查了一次函数的性质.一次函数y=kx+b的图象经过的象限由k、b的值共同决定,有六种情况:
①当k>0,b>0,函数y=kx+b的图象经过第一、二、三象限,y的值随x的值增大而增大;
②当k>0,b<0,函数y=kx+b的图象经过第一、三、四象限,y的值随x的值增大而增大;
③当k<0,b>0时,函数y=kx+b的图象经过第一、二、四象限,y的值随x的值增大而减小;
④当k<0,b<0时,函数y=kx+b的图象经过第二、三、四象限,y的值随x的值增大而减小;
⑤当k>0,b=0,函数y=kx+b的图象经过第一、三象限;
⑥当k<0,b=0,函数y=kx+b的图象经过第二、四象限.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知M、N两点关于y轴对称,且点M在反比例函数 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( )
 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( )A.有最小值,且最小值是 | B.有最大值,且最大值是 |
C.有最大值,且最大值是 | D.有最小值,且最小值是 |
已知M、N两点关于y轴对称,且点M在反比例函数 的图象上,点N在一次函 数
的图象上,点N在一次函 数 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数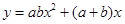 ( )
( )
A.有最小值,且最小值是 | B.有最大值,且最大值是 |
C.有最大值,且最大值是 | D.有最小值,且最小值是 |
 的图象上,点N在一次函 数
的图象上,点N在一次函 数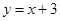 的图象上,设点M的坐标为(a,b),则二次函数
的图象上,设点M的坐标为(a,b),则二次函数 ( )
( ) B.有最大值,且最大值是
B.有最大值,且最大值是 D.有最小值,且最小值是
D.有最小值,且最小值是