题目内容
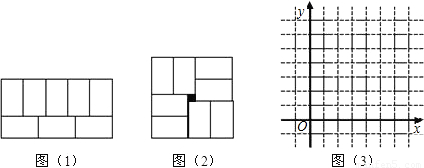
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图(1).然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个小正方形(阴影部分),假设长方形的长为![]() ,宽为
,宽为![]() ,且
,且![]() .
.

(1)求图(1)中![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若阴影小正方形边长为1,求图(2)中![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在图(3)中作出(1)、(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上研究完成下表:
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
|
|
| 6 |
|
| … |
|
|
| 10 |
|
| … |
观察上表,设图(2)中小正方形边长为![]() ,请分别猜想
,请分别猜想![]() 与
与![]() 、
、![]() 与
与![]() 的关系,并证明你的猜
的关系,并证明你的猜
(1)![]() (2)
(2)![]() (3)见解析(4)
(3)见解析(4)![]()
解析:(1)由图(1)得:![]()
![]() ………………2分
………………2分
(2)由图(2)得![]() ………………4分
………………4分
(3)画图(未注意自变量取值范围扣1分)
交点坐标(3,5) ………………7分
实际意义解答不唯一:瓷砖的长为5,宽为3时,能围成图(1),图(2)的图形且小正方形边长为1. ……8分
(4)
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
|
| 3 | 6 | 9 | 12 | … |
|
| 5 | 10 | 15 | 20 | … |
猜想:![]() ,
,![]() ………………………………………………10分
………………………………………………10分
证明:由图(1)(2)知 ,解得
,解得![]() ……………………………………12分
……………………………………12分
想.
(1)、由图可得
(2)根据小长方形的面积×8+小正方形的面积=大长方形的面积,列出方程即可得出
(3)画图时注意自变量取值范围,实际意义解答不唯一,只要符合题意即可
(4)由表可知x是3的倍数,y是5的倍数

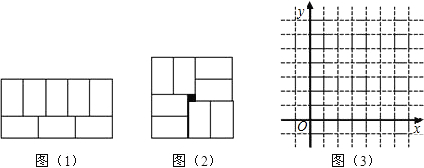
(1)请你求出图1中y与x的函数关系式;
(2)求出图2中y与x的函数关系式;
(3)在图3中作出两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上讨论完成下表,观察x与y的关系,回答:如果给你任意8个相同的长方形,你能否拼成类似图1和图2的图形?说出你的理由.
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
| x | 3 | 6 | 9 | 12 | … |
| y | 5 | 10 | 15 | 20 | … |
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图(1).然后,他用这8块瓷砖又拼出一个正方形,如图(2),中间恰好空出一个小正方形(阴影部分),假设长方形的长为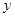 ,宽为
,宽为 ,且
,且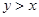 .
.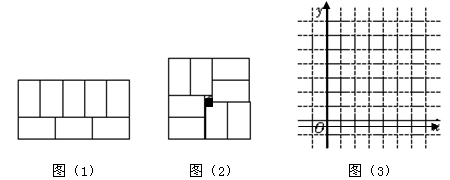
(1)求图(1)中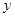 与
与 的函数关系式;
的函数关系式;
(2)若阴影小正方形边长为1,求图(2)中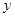 与
与 的函数关系式;
的函数关系式;
(3)在图(3)中作出(1)、(2)中两个函数的图象,写出交点坐标,并解释交点坐标的实际意义;
(4)根据以上研究完成下表:
| 图(2)中小正方形边长 | 1 | 2 | 3 | 4 | … |
 | | 6 | | | … |
 | | 10 | | | … |
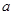 ,请分别猜想
,请分别猜想 与
与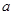 、
、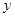 与
与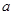 的关系,并证明你的猜
的关系,并证明你的猜 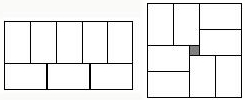 这张师傅在铺地板时发现:用8个大小一样的长方形瓷砖恰好可以拼成一个大的长方形(如图),然后,他用这8块瓷砖七拼八凑,又拼出了一个正方形,中间还留下一个2cm×2cm的小正方形(阴影部分).请你根据提供的信息,求出这些长方形的长和宽.
这张师傅在铺地板时发现:用8个大小一样的长方形瓷砖恰好可以拼成一个大的长方形(如图),然后,他用这8块瓷砖七拼八凑,又拼出了一个正方形,中间还留下一个2cm×2cm的小正方形(阴影部分).请你根据提供的信息,求出这些长方形的长和宽. 张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图,中间恰好空出一个边长为1的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,请写出图中y与x的函数关系式:
张师傅在铺地板时发现,用8块大小一样的长方形瓷砖恰好可以拼成一个大的长方形,如图,中间恰好空出一个边长为1的小正方形(阴影部分),假设小长方形的长为y,宽为x,且y>x,请写出图中y与x的函数关系式: