题目内容
【题目】如图,正方形ABFG和正方形CDEF中,使点B、C的坐标分别为(0,0)和(4,0).
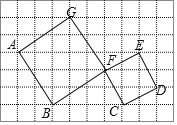
(1)在图中建立平面直角坐标系;
(2)写出A点的坐标;
(3)画出正方形EFCD左平移2个单位,上平移1个单位后的正方形E′F′C′D′.
【答案】(1)平面直角坐标系如图所示,见解析;(2)A(﹣2,3);(3)如图所示,正方形E′F′C′D′即为所求.见解析.
【解析】
(1)根据点B、C的坐标分别为(0,0)和(4,0),即可得到直角坐标系;
(2)根据A点的位置,即可得到其坐标;
(3)根据正方形EFCD左平移2个单位,上平移1个单位,即可得到正方形E′F′C′D′.
解:(1)平面直角坐标系如图所示,

(2)由图可得,A(﹣2,3);
(3)如图所示,正方形E′F′C′D′即为所求.

练习册系列答案
相关题目
【题目】为了解某市市民“绿色出行”方式的情况,某校数学兴趣小组以问卷调查的形式,随机调查了某市部分出行市民的主要出行方式(参与问卷调查的市民都只从以下五个种类中选择一类),并将调查结果绘制成如下不完整的统计图.
种类 | A | B | C | D | E |
出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |

根据以上信息,回答下列问题:
(1)参与本次问卷调查的市民共有 人,其中选择B类的人数有 人;
(2)在扇形统计图中,求A类对应扇形圆心角α的度数,并补全条形统计图;
(3)该市约有12万人出行,若将A,B,C这三类出行方式均视为“绿色出行”方式,请估计该市“绿色出行”方式的人数.