题目内容
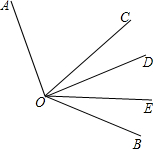 如图.已知OC是∠AOB的平分线,OE是∠BOD的平分线,若∠COE=45°,求∠AOD的度数.
如图.已知OC是∠AOB的平分线,OE是∠BOD的平分线,若∠COE=45°,求∠AOD的度数.分析:根据角平分线的定义可得∠BOC=
∠AOB,∠BOE=
∠BOD,然后根据∠COE=∠BOC-∠BOE代入整理并求解即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵OC是∠AOB的平分线,OE是∠BOD的平分线,
∴∠BOC=
∠AOB=
(∠AOD+∠BOD),∠BOE=
∠BOD,
∴∠COE=∠BOC-∠BOE=
(∠AOD+∠BOD)-
∠BOD=
∠AOD,
∵∠COE=45°,
∴
∠AOD=45°,
∴∠AOD=90°.
∴∠BOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠COE=∠BOC-∠BOE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵∠COE=45°,
∴
| 1 |
| 2 |
∴∠AOD=90°.
点评:本题考查了角的计算,角平分线的定义,熟记概念并整理出∠COE的表达式是解题的关键.

练习册系列答案
相关题目
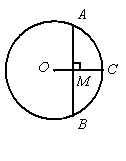
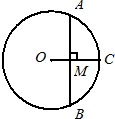 如图,已知OC是⊙O的半径,弦AB=6,AB⊥OC,垂足为M,且CM=2.
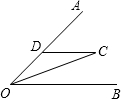
如图,已知OC是⊙O的半径,弦AB=6,AB⊥OC,垂足为M,且CM=2.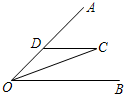 14、如图,已知OC是∠AOB的平分线,DC∥OB,那么△DOC一定是
14、如图,已知OC是∠AOB的平分线,DC∥OB,那么△DOC一定是