题目内容
（2012•福州）如图，从热气球C处测得地面A、B两点的俯角分别是30°、45°，如果此时热气球C处的高度CD为100米，点A、D、B在同一直线上，则AB两点的距离是（ ）分析：图中两个直角三角形中，都是知道已知角和对边，根据正切函数求出邻边后，相加求和即可．
解答：解：由已知，得∠A=30°，∠B=45°，CD=100，
∵CD⊥AB于点D．
∴在Rt△ACD中，∠CDA=90°，tanA=
，
∴AD=
=
=100
在Rt△BCD中，∠CDB=90°，∠B=45°
∴DB=CD=100米，
∴AB=AD+DB=100
+100=100（
+1）米．
故选D．
∵CD⊥AB于点D．
∴在Rt△ACD中，∠CDA=90°，tanA=
| CD |
| AD |
∴AD=
| CD |
| tanA |
| 100 | ||||
|
| 3 |
在Rt△BCD中，∠CDB=90°，∠B=45°
∴DB=CD=100米，
∴AB=AD+DB=100
| 3 |
| 3 |
故选D．
点评：本题考查了解直角三角形的应用，解决本题的关键是利用CD为直角△ABC斜边上的高，将三角形分成两个三角形，然后求解．分别在两三角形中求出AD与BD的长．
练习册系列答案
相关题目
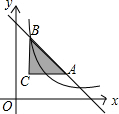（2012•福州）如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y=-x+6于A、B两点，若反比例函数y=
（2012•福州）如图是由4个大小相同的正方形组合而成的几何体，其主视图是（ ）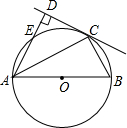
（2012•福州） 如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的切线互相垂直，垂足为D，AD交⊙O于点E．