题目内容
已知圆锥的全面积为10πcm2,侧面展开图的圆心角为40°,则该圆锥底面上的高为
- A.9cm
- B.
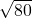 cm
cm - C.
 cm
cm - D.
 cm
cm
B
分析:设出圆锥的底面半径与母线长,利用圆锥的底面周长等于圆锥的侧面展开图的弧长可得到圆锥的底面半径与母线长的关系,进而利用圆锥的全面积可求得圆锥的底面半径,进而求得母线长,利用勾股定理即可求得圆锥底面上的高.
解答:设圆锥的底面半径为r,母线长为R,
∴2πr= ,
,
解得R=9r,
∵圆锥的全面积为10π,
∴π×r2+π×r×9r=10π,
解得r=1cm,
∴R=9cm,
∴该圆锥底面上的高为 =
=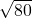 cm.
cm.
故选B.
点评:用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥全面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长;圆锥的高,母线长,底面半径组成直角三角形.
分析:设出圆锥的底面半径与母线长,利用圆锥的底面周长等于圆锥的侧面展开图的弧长可得到圆锥的底面半径与母线长的关系,进而利用圆锥的全面积可求得圆锥的底面半径,进而求得母线长,利用勾股定理即可求得圆锥底面上的高.
解答:设圆锥的底面半径为r,母线长为R,
∴2πr=
 ,
,解得R=9r,
∵圆锥的全面积为10π,
∴π×r2+π×r×9r=10π,
解得r=1cm,
∴R=9cm,
∴该圆锥底面上的高为
 =
=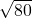 cm.
cm.故选B.
点评:用到的知识点为:圆锥的侧面展开图的弧长等于圆锥的底面周长;圆锥全面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长;圆锥的高,母线长,底面半径组成直角三角形.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
已知圆锥的全面积为10πcm2,侧面展开图的圆心角为40°,则该圆锥底面上的高为( )
| A、9cm | ||||
B、
| ||||
C、
| ||||
D、
|
 cm
cm cm
cm cm
cm