题目内容
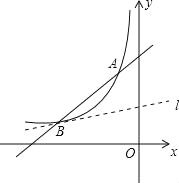
【题目】(2016 广东省茂名市第22题)如图,一次函数y=x+b的图象与反比例函数y=![]() (k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(k为常数,k≠0)的图象交于点A(﹣1,4)和点B(a,1).
(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
【答案】(1)、y=-![]() ;a=-4,b=5;(2)、(-
;a=-4,b=5;(2)、(-![]() ,2)
,2)
【解析】
试题分析:(1)、由点A的坐标结合反比例函数图象上点的坐标特征,即可求出k值,从而得出反比例函数解析式;再将点A、B坐标分别代入一次函数y=x+b中得出关于a、b的二元一次方程组,解方程组即可得出结论;(2)、连接AO,设线段AO与直线l相交于点M.由A、O两点关于直线l对称,可得出点M为线段AO的中点,再结合点A、O的坐标即可得出结论.
试题解析:(1)、∵点A(﹣1,4)在反比例函数y=![]() (k为常数,k≠0)的图象上,
(k为常数,k≠0)的图象上,
∴k=﹣1×4=﹣4, ∴反比例函数解析式为y=﹣![]() .
.
把点A(﹣1,4)、B(a,1)分别代入y=x+b中,
得:![]() ,解得:
,解得:![]() .
.
(2)、连接AO,设线段AO与直线l相交于点M,如图所示. ∵A、O两点关于直线l对称,
∴点M为线段OA的中点, ∵点A(﹣1,4)、O(0,0), ∴点M的坐标为(﹣![]() ,2).
,2).
∴直线l与线段AO的交点坐标为(﹣![]() ,2).
,2).


练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
