��Ŀ����
��2012•��������ͼ������ABCD�ı߳�Ϊ2cm����DAB=60�㣮��P��A���������
cm/s���ٶȣ���AC��C�������˶������ͬʱ����QҲ��A���������1cm/s���ٶȣ�������AB�������˶�����P�˶���C��ʱ��P��Q��ֹͣ�˶���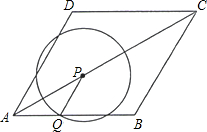 ���P�˶���ʱ��Ϊts��
���P�˶���ʱ��Ϊts��
��1����P����A��Cʱ����˵��PQ��BC��
��2����PΪԲ�ġ�PQ��Ϊ�뾶��Բ�����ʣ��������˶������У�tΪ������ֵʱ����P���BC�ֱ���1���������2�������㣿
| 3 |
 ���P�˶���ʱ��Ϊts��
���P�˶���ʱ��Ϊts����1����P����A��Cʱ����˵��PQ��BC��
��2����PΪԲ�ġ�PQ��Ϊ�뾶��Բ�����ʣ��������˶������У�tΪ������ֵʱ����P���BC�ֱ���1���������2�������㣿
��������1������BD��AC��O������ֱ��������AOB���������εĶԽ����ഹֱ���Խ���ƽ�ֶԽǡ��ڱ���ȵ�������֪��PAQ�ס�CAB��Ȼ����ݡ����������εĶ�Ӧ����ȡ�֤�á�APQ=��ACB��������ƽ���ߵ��ж�������ͬλ����ȣ���ֱ��ƽ�С�����֤�ý��ۣ�
��2����ͼ2����P��BC���ڵ�M������PM������Rt��CPM����Rt��CPM��������ǵ����Ǻ���ֵ���PM=
PC=
-
t��Ȼ�����PM=PQ=AQ=t�г�����t�ķ��̣�ͨ���ⷽ�̼������t��ֵ��
��ͼ3����P����B����ʱPQ=PB�����ݵȱ������ε��ж�������֪��PQBΪ�ȱ������Σ�Ȼ���ɵȱ������ε������Լ���2�������t��ֵ��ȷ����ʱt��ȡֵ��Χ��
��ͼ4����P����C����ʱPC=PQ���ݴ˵�����ϵ�г�����t�ķ��̣�ͨ���ⷽ�����t��ֵ��
��2����ͼ2����P��BC���ڵ�M������PM������Rt��CPM����Rt��CPM��������ǵ����Ǻ���ֵ���PM=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
��ͼ3����P����B����ʱPQ=PB�����ݵȱ������ε��ж�������֪��PQBΪ�ȱ������Σ�Ȼ���ɵȱ������ε������Լ���2�������t��ֵ��ȷ����ʱt��ȡֵ��Χ��
��ͼ4����P����C����ʱPC=PQ���ݴ˵�����ϵ�г�����t�ķ��̣�ͨ���ⷽ�����t��ֵ��
��� �⣺��1�����ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm��
�⣺��1�����ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm��
��AB=BC=2����BAC=
��DAB��
�֡ߡ�DAB=60�㣨��֪����
���BAC=��BCA=30�㣻
��ͼ1������BD��AC��O��
���ı���ABCD�����Σ�
��AC��BD��OA=
AC��
��OB=
AB=1��30������Ե�ֱ�DZ���б�ߵ�һ�룩��
��OA=
��cm����AC=2OA=2
��cm����
�˶�ts��AP=
t��AQ=t��
��
=
=
�֡ߡ�PAQ=��CAB��
���PAQ�ס�CAB��
���APQ=��ACB�����������εĶ�Ӧ����ȣ���
��PQ��BC��ͬλ����ȣ���ֱ��ƽ�У���5��
��2����ͼ2����P��BC���ڵ�M������PM����PM��BC��
��Rt��CPM�У��ߡ�PCM=30�㣬��PM=
PC=
-
t
��PM=PQ=AQ=t����
-
t=t
���t=4
-6����ʱ��P���BC��һ�������㣻
��ͼ3����P����B����ʱPQ=PB��
�ߡ�PQB=��PAQ+��APQ=60��
���PQBΪ�ȱ������Σ���QB=PQ=AQ=t����t=1
����4
-6��t��1ʱ����P���BC��2�������㣮
��ͼ4����P����C����ʱPC=PQ����2
-
t=t����t=3-
��
�൱1��t��3-
ʱ����P���BC��һ�������㣬
����P�˶�����C����t=2ʱ����P����B����ʱ����P���BC��һ�������㣬
�൱t=4
-6��1��t��3-
��t=2ʱ����P������ABCD�ı�BC��1�������㣻
��4
-6��t��1ʱ����P���BC��2�������㣮
 �⣺��1�����ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm��
�⣺��1�����ı���ABCD�����Σ�������ABCD�ı߳�Ϊ2cm����AB=BC=2����BAC=
| 1 |
| 2 |
�֡ߡ�DAB=60�㣨��֪����
���BAC=��BCA=30�㣻
��ͼ1������BD��AC��O��

���ı���ABCD�����Σ�
��AC��BD��OA=
| 1 |
| 2 |
��OB=
| 1 |
| 2 |
��OA=
| 3 |
| 3 |
�˶�ts��AP=
| 3 |
��
| AP |
| AQ |
| AC |
| AB |
| 3 |
�֡ߡ�PAQ=��CAB��
���PAQ�ס�CAB��
���APQ=��ACB�����������εĶ�Ӧ����ȣ���
��PQ��BC��ͬλ����ȣ���ֱ��ƽ�У���5��
��2����ͼ2����P��BC���ڵ�M������PM����PM��BC��
��Rt��CPM�У��ߡ�PCM=30�㣬��PM=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
��PM=PQ=AQ=t����
| 3 |
| ||
| 2 |
���t=4
| 3 |
��ͼ3����P����B����ʱPQ=PB��
�ߡ�PQB=��PAQ+��APQ=60��
���PQBΪ�ȱ������Σ���QB=PQ=AQ=t����t=1
����4
| 3 |
��ͼ4����P����C����ʱPC=PQ����2
| 3 |
| 3 |
| 3 |
�൱1��t��3-
| 3 |
����P�˶�����C����t=2ʱ����P����B����ʱ����P���BC��һ�������㣬
�൱t=4
| 3 |
| 3 |
��4
| 3 |
�����������ۺϿ��������ε����ʡ�ֱ����Բ��λ�ù�ϵ�Լ����������ε��ж������ʣ����2����ʱ�����ݡ�P���˶�������ȷ��t��ֵ���Է�©�⣮

��ϰ��ϵ�д�
�����Ŀ
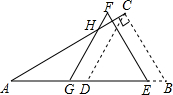 ��2012•������ ��ͼ����ABC�У���ACB=90�㣬AB=8cm��D��AB���е㣮�ֽ���BCD��BA����ƽ��1cm���õ���EFG��FG��AC��H����GH�ij�����
��2012•������ ��ͼ����ABC�У���ACB=90�㣬AB=8cm��D��AB���е㣮�ֽ���BCD��BA����ƽ��1cm���õ���EFG��FG��AC��H����GH�ij�����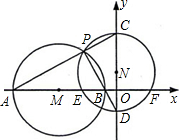 ��2012•��������ͼ����M��-5��0��ΪԲ�ġ�4Ϊ�뾶��Բ��x�ύ��A��B���㣬P�ǡ�M������A��B��һ���㣬ֱ��PA��PB�ֱ�y����C��D����CDΪֱ���ġ�N��x�ύ��E��F����EF�ij���������
��2012•��������ͼ����M��-5��0��ΪԲ�ġ�4Ϊ�뾶��Բ��x�ύ��A��B���㣬P�ǡ�M������A��B��һ���㣬ֱ��PA��PB�ֱ�y����C��D����CDΪֱ���ġ�N��x�ύ��E��F����EF�ij��������� ��2012•��������ͼ������ABCD�У�AD��BC��AD=3��AB=5��BC=9��CD�Ĵ�ֱƽ���߽�BC��E������DE�����ı�
��2012•��������ͼ������ABCD�У�AD��BC��AD=3��AB=5��BC=9��CD�Ĵ�ֱƽ���߽�BC��E������DE�����ı� ��2012•��������ͼ���ڱ߳�Ϊ24cm��������ֽƬABCD�ϣ���ȥͼ����Ӱ���ֵ��ĸ�ȫ�ȵĵ���ֱ�������Σ�����ͼ�е����������۳�һ����������״�İ�װ�У�A��B��C��D�ĸ����������غ����ϵ�����һ�㣩����֪E��F��AB���ϣ��DZ���ȥ��һ������ֱ��������б�ߵ������˵㣬��AE=BF=x��cm����
��2012•��������ͼ���ڱ߳�Ϊ24cm��������ֽƬABCD�ϣ���ȥͼ����Ӱ���ֵ��ĸ�ȫ�ȵĵ���ֱ�������Σ�����ͼ�е����������۳�һ����������״�İ�װ�У�A��B��C��D�ĸ����������غ����ϵ�����һ�㣩����֪E��F��AB���ϣ��DZ���ȥ��һ������ֱ��������б�ߵ������˵㣬��AE=BF=x��cm����