Question

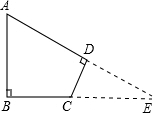
某片绿地的形状如图所示，其中∠A=60°，AB⊥BC，AD⊥CD，AB=200m，CD=100m，求AD、BC的长．（精确到1m，

3

≈1.732）

Answer 1

分析：延长AD，交BC的延长线于点E，则在直角△ABE与直角△CDE中，根据三角函数就可求得BE，与CE的长，就可求得AD与BC的长．

解答：解：解法一：
如图，延长AD，交BC的延长线于点E，

在Rt△ABE中，由AB=200m，∠A=60°得BE=AB•tanA=200

3

m
AE=

AB

cos60°

=400m
在Rt△CDE中，由CD=100m，
∠CED=90°-∠A=30°，得CE=2CD=200m，
DE=

CD

tan∠CED

=100

3

m
∴AD=AE-DE=400-100

3

m≈227m
BC=BE-CE=200

3

-200≈146m
答：AD的长约为227m，BC的长约为146m；
解法二：
如图，过点D作矩形ABEF．

设AD=x，
在Rt△ADF中，∠DAF=90°-60°=30°，
∴DF=

1

2

AD=

1

2

x，AF=

3

2

x
在Rt△CDE中，∠CDE=30°．则CE=

1

2

CD=50m，DE=

3

2

CD=50

3

m
∵DE+DF=AB
∴50

3

+

1

2

x=200，得x=400-100

3

，即AD≈227m
∵BC+CE=AF，
∴BC=

3

2

x-50=

3

2

(400-100

3

)-50=200

3

-200≈146m
答：AD的长约为227m，BC的长约为146m．

点评：不规则图形可以转化为直角三角形的计算，解题的关键是正确作辅助线．