题目内容
如图，D是等腰三角形ABC底边BC的中点，DE⊥AB，DF⊥AC．
试说明：DE=DF．
证明：连接AD，∵D是等腰三角形ABC底边BC的中点，
∴AD是∠BAC的平分线，
∵DE⊥AB，DF⊥AC，
∴DE=DF．
分析：连接AD，根据等腰三角形三线合一的性质可得AD是∠BAC的平分线，然后根据角平分线上的点到角的两边的距离相等证明即可．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，等腰三角形三线合一的性质，熟记性质并作辅助线是解题的关键．
练习册系列答案
相关题目
24、如图，AD是等腰三角形ABC的底边BC上的高，DE∥AB，交AC于点E，判断△ADE是不是等腰三角形，并说明理由．
于点E，连接BE与AC交于点F．
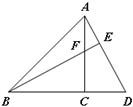22、如图，△ABC是等腰三角形，∠ACB=90°，延长BC到D，连接AD，过点B作BE⊥AD于E，交AC于F，在这个图形中，哪两个三角形可以看成是其中一个三角形沿着某一点旋转而得到的？试说明理由．
如图，△ABC是等腰三角形，AB=AC，
如图，△ABC是等腰三角形，∠ABC=120°，点P是底边AC上一个动点，M、N分别是AB、BC的中点，若PM+PN的最小值为4，则下列各结论中，正确的结论是（ ）