题目内容
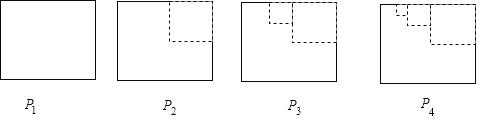
【题目】如图，P1是一块边长为1的正方形纸板，在P1的右上端剪去一个边长为
的正方形后得到图形P2，然后依次剪去一个更小的正方形（其边长为前一个被剪去的正方形边长的一半）得到图形P3、P4、P5…，记纸板Pn的面积为Sn，则Sn﹣Sn+1的值为（ ）
A.（）nB.（
）nC.（）n+1D.（）2n﹣1
【答案】B
【解析】
根据题目中的图形，可以写出前几个图形的面积，从而可以得到Sn-Sn+1的值，本题得以解决．
解：由题意可得，
S1＝1，
S2＝1﹣（
）2，
S3＝1﹣（）2﹣（
）2＝1﹣（）2﹣（）4，
S4＝1﹣（）2﹣（）4﹣（）6，
…，
则Sn﹣Sn+1＝[1﹣（）2﹣（）4﹣（）6，﹣…﹣（）2n﹣2]﹣[1﹣（）2﹣（）4﹣（）6﹣…﹣（）2n]＝（）2n＝（
）n，
故选：B．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
