题目内容
将矩形![]() 置于平面直角坐标系中,点
置于平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
![]() ,点
,点![]()
![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿
沿![]() 折叠压平,使点
折叠压平,使点![]() 落在坐标平面内,设点
落在坐标平面内,设点![]() 的对应点为点
的对应点为点![]() .
.
(1)当![]() 时,点
时,点![]() 的坐标为 ,点
的坐标为 ,点![]() 的坐标为 ;
的坐标为 ;
(2)随着![]() 的变化,试探索:点
的变化,试探索:点![]() 能否恰好落在
能否恰好落在![]() 轴上?若能,请求出
轴上?若能,请求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
(3)如图9,若点![]() 的纵坐标为
的纵坐标为![]() ,抛物线
,抛物线![]() (
(![]() 且
且![]() 为常数)的顶点落在
为常数)的顶点落在![]() 的内部,求
的内部,求![]() 的取值范围.
的取值范围.
 |
解:(1) 点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;…………………………………………3分
;…………………………………………3分
(2)点![]() 能恰好落在
能恰好落在![]() 轴上.理由如下:
轴上.理由如下:
![]() 四边形
四边形![]() 为矩形
为矩形
![]() ,
,![]() …………………………………………………4分
…………………………………………………4分
由折叠的性质可得:![]() ,
,![]() ,
,
如图9-1,假设点![]() 恰好落在
恰好落在![]() 轴上,在
轴上,在![]() 中,由
中,由
勾股定理可得![]() ,
,
则有![]() ……………………5分
……………………5分
 在
在![]() 中,
中,
![]() 即
即![]()
解得![]() ……………………………………7分
……………………………………7分
(3)解法一:如图9-2,过点![]() 作
作![]() 于
于![]() ,
,![]()
分别与 ![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 于
于
点![]() ,则
,则![]() ,
,
 在
在![]() 中,由勾股定理可得
中,由勾股定理可得
![]()
![]()
![]() ………………………8分
………………………8分
在![]() 中,
中,![]() ,
,
![]() ,
,![]()
![]()
![]() 解得
解得![]() …………………………………………………9分
…………………………………………………9分
![]()
![]() ,
,![]() ,
,![]() (
(![]() ,-1)
,-1)
![]()
![]() ,
,![]()
![]()
![]() ∽
∽![]()
![]()
![]() 即
即![]() 解得
解得![]()
![]()
![]()
![]() 点
点![]() 的纵坐标为
的纵坐标为![]() …………………………………………………………………………10分
…………………………………………………………………………10分
![]()
![]()
![]() 此抛物线的顶点必在直线
此抛物线的顶点必在直线![]() 上 ……………………………………………………11分
上 ……………………………………………………11分
又![]() 抛物线
抛物线![]() 的顶点落在
的顶点落在![]() 的内部
的内部
![]() 此抛物线的顶点必在
此抛物线的顶点必在![]() 上
上
![]()
![]() ………………………………………………………………………12分
………………………………………………………………………12分
 解得
解得![]()
故![]() 的取值范围为
的取值范围为 ![]() ……………………………………13分
……………………………………13分
解法二:如图9-3,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 分别与
分别与
![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,设
,设![]() 与
与![]() 相交于点
相交于点![]() .
.
![]()
![]() ,
,![]() ,
,![]()
![]()
![]() ≌
≌![]() (AAS)
(AAS)

![]()
![]() ,
,![]()
由勾股定理可得![]()
![]() (以下过程同解法一)
(以下过程同解法一)
解法三:如图9-4,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 分别与
分别与![]() 、
、![]()
交于点![]() 、
、![]() ,作
,作![]() 交
交![]() 延长线于点
延长线于点![]() ,则有
,则有

![]() ,
,
在![]() 中,由勾股定理可得
中,由勾股定理可得
![]()
![]()
![]() …………………………………8分
…………………………………8分
(以下过程同解法一)
解法四:如图9-5,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点
![]() 、交
、交![]() 轴于点
轴于点![]() ,可仿第(2)小题两次利用勾股定
,可仿第(2)小题两次利用勾股定
理求出![]() 的值,也可以利用
的值,也可以利用
![]() ∽
∽![]()
![]() 求出
求出![]() 的值. …………………………9分
的值. …………………………9分
(以下过程同解法一)

 阅读快车系列答案
阅读快车系列答案 如图,矩形ABCD的边长AB=9,AD=3,将此矩形置于平面直角坐标系xOy中,使AB在x轴正半轴上,经过点C的直线
如图,矩形ABCD的边长AB=9,AD=3,将此矩形置于平面直角坐标系xOy中,使AB在x轴正半轴上,经过点C的直线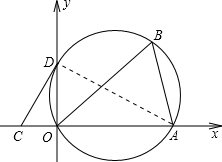 ,0),∠ABO=60度.
,0),∠ABO=60度. 如图,矩形ABCD的边长AB=9,AD=3,将此矩形置于平面直角坐标系xOy中,使AB在x轴正半轴上,经过点C的直线
如图,矩形ABCD的边长AB=9,AD=3,将此矩形置于平面直角坐标系xOy中,使AB在x轴正半轴上,经过点C的直线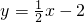 与x轴交于点E,则四边形AECD的面积是________.
与x轴交于点E,则四边形AECD的面积是________. 与x轴交于点E,则四边形AECD的面积是 .
与x轴交于点E,则四边形AECD的面积是 .