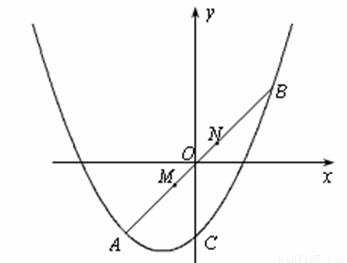
题目内容
(9分)抛物线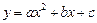 与y轴交于点
与y轴交于点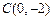 ,与直线
,与直线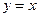
交于点
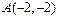 ,
,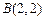 .
.(1)求抛物线的解析式;
(2)如图,线段MN在线段AB上移动(点M与点A不重合,点N与点B不重合),且
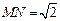 ,若M点的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
,若M点的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.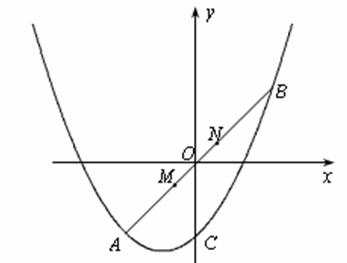
解:(1)抛物线 过点C(0,-2)可得
过点C(0,-2)可得 。
。
把点A(-2,-2),B(2,2)代入 ,整理得
,整理得 ,
,
解得 。
。
∴抛物线的解析式为: 。
。
(2)∵MN= ,点A,B都在直线
,点A,B都在直线 上,MN在线段AB上,M的横坐标为m。
上,MN在线段AB上,M的横坐标为m。
如图1,过点M作x轴的平行线,过点N作y轴的平行线,它们相交于点H。

∴△MHN是等腰直角三角形.∴MH=NH=1。
∴点N的坐标为( ,
, )。
)。
① 如图2,当 时,PM=-m,
时,PM=-m,

 。
。
当四边形PMQN为平行四边形时,PM=NQ.
∴ .
.
解得 (舍去),
(舍去), 。
。
②如图3,当 时,PM=m,
时,PM=m,

 .
.
当四边形PMNQ为平行四边形时,PM=NQ,
∴ 。
。
解得 (舍去),
(舍去), 。
。
∴当 或
或 时,以点P,M,N,Q为顶点的四边形为平行四边形。解析:
时,以点P,M,N,Q为顶点的四边形为平行四边形。解析:
略
 过点C(0,-2)可得
过点C(0,-2)可得 。
。把点A(-2,-2),B(2,2)代入
 ,整理得
,整理得 ,
,解得
 。
。∴抛物线的解析式为:
 。
。(2)∵MN=
 ,点A,B都在直线
,点A,B都在直线 上,MN在线段AB上,M的横坐标为m。
上,MN在线段AB上,M的横坐标为m。如图1,过点M作x轴的平行线,过点N作y轴的平行线,它们相交于点H。

∴△MHN是等腰直角三角形.∴MH=NH=1。
∴点N的坐标为(
 ,
, )。
)。① 如图2,当
 时,PM=-m,
时,PM=-m,
 。
。当四边形PMQN为平行四边形时,PM=NQ.
∴
 .
.解得
 (舍去),
(舍去), 。
。②如图3,当
 时,PM=m,
时,PM=m,
 .
.当四边形PMNQ为平行四边形时,PM=NQ,
∴
 。
。解得
 (舍去),
(舍去), 。
。∴当
 或
或 时,以点P,M,N,Q为顶点的四边形为平行四边形。解析:
时,以点P,M,N,Q为顶点的四边形为平行四边形。解析:略

练习册系列答案
相关题目
 C所对边的长.
C所对边的长.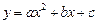 与y轴交于点
与y轴交于点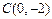 ,与直线
,与直线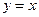
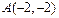 ,
,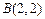 .
.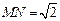 ,若M点的横坐标为m,过点M作
,若M点的横坐标为m,过点M作 x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.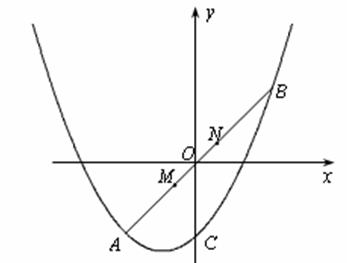
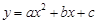 与y轴交于点
与y轴交于点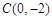 ,与直线
,与直线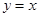
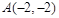 ,
,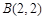 .
.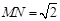 ,若M点的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.
,若M点的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出m的值;若不能,请说明理由.