题目内容
 已知抛物线y=-
已知抛物线y=-| 1 | 2 |
(1)直接写出抛物线的解析式;
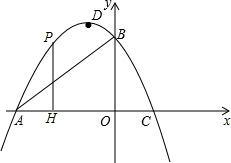
(2)设(1)中的抛物线与x轴的交点为A、C,与y轴的交点为B,求A、C两点的坐标和△ABC的面积;
(3)H是线段OA上一点,过点H作PH⊥x轴,交抛物线于点P,若直线AB把△PAH分成面积相等的两部分,求H点的坐标.
分析:(1)将顶点D(-2,8)直接代入解析式,继而得出这个抛物线的解析式;
(2)由抛物线解析式可求出点A、C、点B的坐标,利用S△ABC=
×AC×OB,即可得出答案;
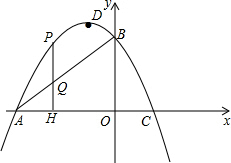
(3)若直线AB分△PAH为面积相等两部分,则需PH与线段BA的交点是线段PH的中点,设H(a,0),则Q(a,a+6),P(a,-
a2-2a+6),根据QH=
PH,可得关于a的方程,解出即可.
(2)由抛物线解析式可求出点A、C、点B的坐标,利用S△ABC=
| 1 |
| 2 |
(3)若直线AB分△PAH为面积相等两部分,则需PH与线段BA的交点是线段PH的中点,设H(a,0),则Q(a,a+6),P(a,-
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵抛物线y=-
x2+bx+c的图象的顶点D(-2,8),
∴抛物线的解析式为:y=-
(x+2)2+8=-
x2-2x+6;
(2)∵y=-
(x+2)2+8,令y=0,
∴0=-
(x+2)2+8,
解得:x1=-6,x2=2,
∴A(-6,0),C(2,0),
令x=0,则y=6,
∴B(0,6),
∴S△ABC=
×AC×OB=
×6×8=24;
(3)将A(-6,0),B(0,6)代入y=kx+b,
则
,
解得:
,
∴直线AB的解析式为:y=x+6,
设AB、PH交于Q,设H(a,0),
则Q(a,a+6),P(a,-
a2-2a+6),
若直线AB把△PAH分成面积相等的两部分,则
S△AQH=
S△PAH,
即QH=
PH,
a+6=
×(-
a2-2a+6),
解得:a1=-2,a2=-6(舍去),
∴H点坐标为:(-2,0).
| 1 |
| 2 |
∴抛物线的解析式为:y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵y=-
| 1 |
| 2 |
∴0=-
| 1 |
| 2 |
解得:x1=-6,x2=2,
∴A(-6,0),C(2,0),
令x=0,则y=6,
∴B(0,6),
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(3)将A(-6,0),B(0,6)代入y=kx+b,
则
|
解得:
|

∴直线AB的解析式为:y=x+6,
设AB、PH交于Q,设H(a,0),
则Q(a,a+6),P(a,-
| 1 |
| 2 |
若直线AB把△PAH分成面积相等的两部分,则
S△AQH=
| 1 |
| 2 |
即QH=
| 1 |
| 2 |
a+6=
| 1 |
| 2 |
| 1 |
| 2 |
解得:a1=-2,a2=-6(舍去),
∴H点坐标为:(-2,0).
点评:此题考查了一元二次方程的解法、二次函数解析式的确定、图形面积的求法、函数图象上点的坐标意义等基础知识,难度不大.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 已知抛物线y=-
已知抛物线y=-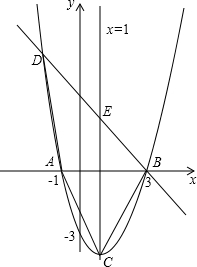 点B在A点的右侧;交y轴于(0,-3).
点B在A点的右侧;交y轴于(0,-3).