题目内容
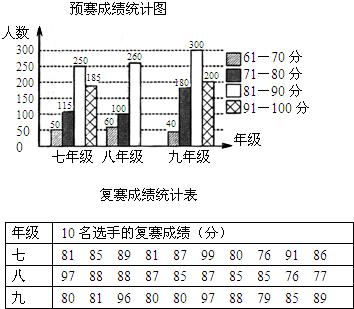
日前，重庆南开中学开展了“遵守交通规则，做文明南开人”教育活动，某班数学兴趣小组的同学深受教育，在南开苑路口以10分钟为一个时间段统计了行人乱穿公路的情况，绘制了如下两幅不完整的统计图：（其中A表示“l0分钟内无人乱穿公路”，B表示“10分钟内有一人乱穿公路”，C表示“10分钟内有二人乱穿公路”，D表示“l0分钟内有三人乱穿公路”）
（1）根据上图，该数学兴趣小组共统计了______个时间段，并将条形统计图补充完整；
（2）平均每个时间段有______人乱穿公路；
（3）该数学兴趣小组的同学随后又观察到4名行人同时乱穿公路，其中有一名学生．他们打算从这4人中随机选出两位进行遵守交通规则的劝导．请求出选出的两位中恰好没有学生的概率．
解：（1）根据题意得：2÷20%=10（个），即该数学兴趣小组共统计了10个时间段；
B有10×30%=3（个），D有10-（4+3+2）=1（个），补全条形统计图，如图所示：
故答案为：10；
（2）根据题意得：
×（3×1+2×2+1×3）=1（人），即平均每个时间段有1人乱穿公路；
故答案为：1；
（3）列表如下：（其中1表示学生）
得到所有等可能的情况数为12种，其中恰好两位中没有学生的情况有6种，
则P=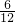
=
．
分析：（1）由C的人数除以所占的百分比求出时间段的总数，进而确定出B与D的人数，补全条形统计图即可；
（2）求出加权平均数即可；
（3）列表得出所有等可能的情况数，找出两位恰好没有学生的情况数，求出所求概率即可．
点评：此题考查了条形统计图，扇形统计图，以及列表法与树状图法，弄清题意是解本题的关键．
B有10×30%=3（个），D有10-（4+3+2）=1（个），补全条形统计图，如图所示：
故答案为：10；
（2）根据题意得：
×（3×1+2×2+1×3）=1（人），即平均每个时间段有1人乱穿公路；故答案为：1；
（3）列表如下：（其中1表示学生）
| 1 | 2 | 3 | 4 | |
| 1 | --- | （2，1） | （3，1） | （4，1） |
| 2 | （1，2） | --- | （3，2） | （4，2） |
| 3 | （1，3） | （2，3） | --- | （4，3） |
| 4 | （1，4） | （2，4） | （3，4） | --- |
则P=
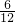=．分析：（1）由C的人数除以所占的百分比求出时间段的总数，进而确定出B与D的人数，补全条形统计图即可；
（2）求出加权平均数即可；
（3）列表得出所有等可能的情况数，找出两位恰好没有学生的情况数，求出所求概率即可．
点评：此题考查了条形统计图，扇形统计图，以及列表法与树状图法，弄清题意是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
频率分布直方图，已知图中从左到右的前四个小组的频率分别是：0.08，0.16，0.20，0.32，第一小组的频数是4．