题目内容
【题目】探究函数y=x+ 
的图象与性质
（1）函数y=x+ 的自变量x的取值范围是；
（2）下列四个函数图象中，函数y=x+ 的图象大致是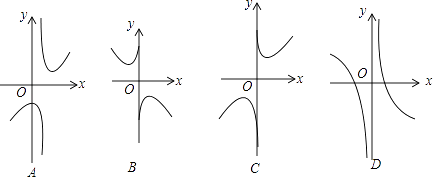
（3）对于函数y=x+ ，求当x＞0时，y的取值范围．
请将下面求解此问题的过程补充完整：
解：∵x＞0
∴y=x+
=（ 
）2+（ 
）2
=（ ﹣ ）2+
∵（ ﹣ ）2≥0，
∴y ．
（4）若函数y= 
，则y的取值范围是
【答案】
（1）x≠0
（2）C
（3）6；≥6
【拓展运用】
（4）y≤﹣11或y≥1
【解析】解：（1）∵在y=x+ 
中，x≠0，
∴x的取值范围是x≠0．
所以答案是：x≠0．（2）∵x≠0，
∴A中图象不符合题意；
∵当x＞0时，x+ ＞0，
当x＜0时，x+ ＜0，
∴函数y=x+ 的图象在第一、三象限，
∴B、D中图象不符合题意，
故选C．（3）解：∵x＞0，
∴y=x+ ，
=（ 
）2+（ 
）2 ，
=（ ﹣ ）2+6，
∵（ ﹣ ）2≥0，
∴y≥6．
所以答案是：6；≥6．（4）y= 
=x+ ﹣5．
由（3）可知：当x＞0时，x+ ≥6；
当x＜0时，x+ ≤﹣6．
∴y=x+ ﹣5≥6﹣5=1，y=x+ ﹣5≤﹣6﹣5=﹣11．
y的取值范围是y≤﹣11或y≥1．
所以答案是：y≤﹣11或y≥1．
【考点精析】根据题目的已知条件，利用反比例函数的性质的相关知识可以得到问题的答案，需要掌握性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
