题目内容
如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0),与y轴交于点C(0,3).
(1)求抛物线的解析式及顶点D的坐标;
(2)若P为线段BD上的一个动点,点P的横坐标为m,试用含m的代数式表示点P的纵坐标;
(3)过点P作PM⊥x轴于点M,求四边形PMAC的面积的最大值和此时点P的坐标;
(4)若点F是第一象限抛物线上的一个动点,过点F作FQ∥AC交x轴于点Q.当点F的坐标为______时,四边形FQAC是平行四边形;当点F的坐标为______时,四边形FQAC是等腰梯形(直接写出结果,不写求解过程).

解:(1)∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(3,0),
∴可设抛物线的解析式为:y=a(x+1)(x-3)
又∵抛物线 与y轴交于点C(0,3),
∴3=a(0+1)(0-3)
∴a=-1
∴y=-(x+1)(x-3)
即抛物线的解析式为:y=-x2+2x+3
∴y=-(x-1)2+4
∴抛物线顶点D的坐标为(1,4);
(2)设直线BD的解析式为:y=kx+b
由B(3,0),D(1,4)得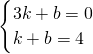
解得 .
.
∴直线BD的解析式为y=-2x+6,
∵点P在直线PD上,点P的横坐标为m
∴点P的纵坐标为:-2m+6;
(3)由(1),(2)知:
OA=1,OC=3,OM=m,PM=-2m+6,
∴S四边形PMAC=S△OAC+S梯形OMPC
=
=
= ,
,
∵ ,
,
∴当 时,四边形PMAC的面积取得最大值为
时,四边形PMAC的面积取得最大值为 ,
,
此时点P的坐标为( ,
, );
);
 (4)①四边形PQAC是平行四边形,如右图①所示.
(4)①四边形PQAC是平行四边形,如右图①所示.
过点P作PE⊥x轴于点E,易证△AOC≌△QEP,
∴yP=PE=CO=3.
又∵CP∥x轴,
则点C(0,3)与点P关于对称轴x=1对称,
∴xP=2.
∴P(2,3).
②四边形PQAC是等腰梯形,如右图②所示.
设P(m,n),P点在抛物线上,则有n=-m2+2m+3.
过P点作PE⊥x轴于点E,则PE=n.
在Rt△OAC中,OA=1,OC=3,
∴AC= ,tan∠CAO=3,cos∠CAO=
,tan∠CAO=3,cos∠CAO= ;
;
∵PQ∥CA,
∴tan∠PQE= =tan∠CAO=3,
=tan∠CAO=3,
∴QE= n,PQ=
n,PQ= =
= n.
n.
过点Q作QM∥PC,交AC于点M,则四边形PCMQ为平行四边形,△QAM为等腰三角形.再过点Q作QN⊥AC于点N.
则有:CM=PQ= n,AN=
n,AN= AM=
AM= (AC-CM)=
(AC-CM)= (1-
(1- n),
n),
AQ= =
= =5(1-
=5(1- n).
n).
又∵AQ=AO+OQ=1+(m- n),
n),
∴5(1- n)=1+(m-
n)=1+(m- n),化简得:n=3-
n),化简得:n=3- m;
m;
又∵P点在抛物线上,有n=-m2+2m+3,
∴-m2+2m+3=3- m,化简得:m2-
m,化简得:m2- m=0,
m=0,
解得m1=0(舍去),m2= ,
,
∴m= ,n=3-
,n=3- m=
m= ,
,
∴P( ,
, ).
).
故答案为:(2,3);( ,
, ).
).
分析:(1)利用待定系数法求出抛物线的解析式,然后化为顶点式求出D点坐标;
(2)利用待定系数法求出直线的解析式,然后将点P的横坐标m代入,即可用含m的代数式表示点P的纵坐标;
(3)本问关键是求出四边形PMAC面积的表达式,这个表达式是关于P点横坐标的二次函数,再利用二次函数求极值的方法求出面积的最大值,并求出P点坐标;
(4)四边形PQAC为平行四边形或等腰梯形时,需要结合几何图形的性质求出P点坐标:
①当四边形PQAC为平行四边形时,如答图1所示.构造全等三角形求出P点的纵坐标,再利用P点与C点关于对称轴x=1对称的特点,求出P点的横坐标;
②当四边形PQAC为平行四边形时,如答图2所示.利用等腰梯形、平行四边形、全等三角形以及线段之间的三角函数关系,求出P点坐标.注意三角函数关系部分,也可以用相似三角形解决.
点评:本题综合考查了诸多重要的知识点,包括:二次函数的图象与性质、待定系数法、二次函数的极值、图形面积的求法、等腰梯形、平行四边形、等腰三角形、三角函数(或相似三角形)等,涉及考点众多,有一定的难度.本题难点在于第(4)问等腰梯形的情形,注意该种情形下求点的坐标的方法.
∴可设抛物线的解析式为:y=a(x+1)(x-3)
又∵抛物线 与y轴交于点C(0,3),
∴3=a(0+1)(0-3)
∴a=-1
∴y=-(x+1)(x-3)
即抛物线的解析式为:y=-x2+2x+3
∴y=-(x-1)2+4
∴抛物线顶点D的坐标为(1,4);
(2)设直线BD的解析式为:y=kx+b
由B(3,0),D(1,4)得
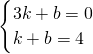
解得
 .
.∴直线BD的解析式为y=-2x+6,
∵点P在直线PD上,点P的横坐标为m
∴点P的纵坐标为:-2m+6;
(3)由(1),(2)知:
OA=1,OC=3,OM=m,PM=-2m+6,
∴S四边形PMAC=S△OAC+S梯形OMPC
=

=

=
 ,
,∵
 ,
,∴当
 时,四边形PMAC的面积取得最大值为
时,四边形PMAC的面积取得最大值为 ,
,此时点P的坐标为(
 ,
, );
); (4)①四边形PQAC是平行四边形,如右图①所示.
(4)①四边形PQAC是平行四边形,如右图①所示.过点P作PE⊥x轴于点E,易证△AOC≌△QEP,
∴yP=PE=CO=3.
又∵CP∥x轴,
则点C(0,3)与点P关于对称轴x=1对称,
∴xP=2.
∴P(2,3).
②四边形PQAC是等腰梯形,如右图②所示.
设P(m,n),P点在抛物线上,则有n=-m2+2m+3.
过P点作PE⊥x轴于点E,则PE=n.

在Rt△OAC中,OA=1,OC=3,
∴AC=
 ,tan∠CAO=3,cos∠CAO=
,tan∠CAO=3,cos∠CAO= ;
;∵PQ∥CA,
∴tan∠PQE=
 =tan∠CAO=3,
=tan∠CAO=3,∴QE=
 n,PQ=
n,PQ= =
= n.
n.过点Q作QM∥PC,交AC于点M,则四边形PCMQ为平行四边形,△QAM为等腰三角形.再过点Q作QN⊥AC于点N.
则有:CM=PQ=
 n,AN=
n,AN= AM=
AM= (AC-CM)=
(AC-CM)= (1-
(1- n),
n),AQ=
 =
= =5(1-
=5(1- n).
n).又∵AQ=AO+OQ=1+(m-
 n),
n),∴5(1-
 n)=1+(m-
n)=1+(m- n),化简得:n=3-
n),化简得:n=3- m;
m;又∵P点在抛物线上,有n=-m2+2m+3,
∴-m2+2m+3=3-
 m,化简得:m2-
m,化简得:m2- m=0,
m=0,解得m1=0(舍去),m2=
 ,
,∴m=
 ,n=3-
,n=3- m=
m= ,
,∴P(
 ,
, ).
).故答案为:(2,3);(
 ,
, ).
).分析:(1)利用待定系数法求出抛物线的解析式,然后化为顶点式求出D点坐标;
(2)利用待定系数法求出直线的解析式,然后将点P的横坐标m代入,即可用含m的代数式表示点P的纵坐标;
(3)本问关键是求出四边形PMAC面积的表达式,这个表达式是关于P点横坐标的二次函数,再利用二次函数求极值的方法求出面积的最大值,并求出P点坐标;
(4)四边形PQAC为平行四边形或等腰梯形时,需要结合几何图形的性质求出P点坐标:
①当四边形PQAC为平行四边形时,如答图1所示.构造全等三角形求出P点的纵坐标,再利用P点与C点关于对称轴x=1对称的特点,求出P点的横坐标;
②当四边形PQAC为平行四边形时,如答图2所示.利用等腰梯形、平行四边形、全等三角形以及线段之间的三角函数关系,求出P点坐标.注意三角函数关系部分,也可以用相似三角形解决.
点评:本题综合考查了诸多重要的知识点,包括:二次函数的图象与性质、待定系数法、二次函数的极值、图形面积的求法、等腰梯形、平行四边形、等腰三角形、三角函数(或相似三角形)等,涉及考点众多,有一定的难度.本题难点在于第(4)问等腰梯形的情形,注意该种情形下求点的坐标的方法.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).