题目内容
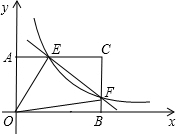
如图,双曲线y=
与直线y=mx相交于A、B两点,M为此双曲线在第一象限内的任一点(M在A点左侧),设直线AM、BM分别与y轴相交于P、Q两点,且p=
,q=
,则p-q的值为______.

| k |
| x |
| MB |
| MQ |
| MA |
| MP |

∵双曲线y=
与直线y=mx相交于A、B两点,
∴设A(m,n)则B(-m,-n),
过A作AN⊥y轴于N,过M作MH⊥y轴于H,过B作BG⊥y轴于G,
则BG=AN=m,
∴MH∥AN∥BG,
∴
=
,
∴p=
=
=1+
=1+
,
∵
=
,
∴
=
,
即1+
=
,
∴q=
=
-1,
∵BG=AN,
∴p-q=(1+
)-(
-1)=2.
故答案为:2.
| k |
| x |

∴设A(m,n)则B(-m,-n),
过A作AN⊥y轴于N,过M作MH⊥y轴于H,过B作BG⊥y轴于G,
则BG=AN=m,
∴MH∥AN∥BG,
∴
| BQ |
| MQ |
| BG |
| MH |
∴p=
| MB |
| MQ |
| MQ+BQ |
| MQ |
| BQ |
| MQ |
| BG |
| MH |
∵
| AP |
| PM |
| AN |
| MH |
∴
| AM+MP |
| MP |
| AN |
| MH |
即1+
| AM |
| MP |
| AN |
| MH |
∴q=
| AM |
| MP |
| AN |
| MH |
∵BG=AN,
∴p-q=(1+
| BG |
| MH |
| AN |
| MH |
故答案为:2.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
 标为4.
标为4.


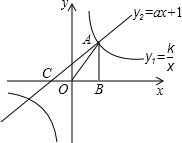
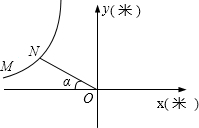 为(
为(