题目内容
 如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′,CE.那么下面结论正确的是( )
如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′,CE.那么下面结论正确的是( )①△ADA′≌△CDE;②直线CE是线段AA′的垂直平分线;③△AEA′是等腰三角形;④S△DEA′=S△B′EA.
| A、①②③ | B、①③④ |
| C、②③④ | D、①②③④ |
考点:旋转的性质
专题:
分析:根据正方形和旋转的性质得∠B′A′C=45°,∠ADC=90°,CB=CB′,CA=CA′,则可判断△A′DE为等腰直角三角形,于是可根据“SAS”证明△ADA′≌△CDE,则可对①进行判断;根据“HL”可证明t△CB′E≌Rt△CDE,得到∠B′CE=∠DCE,即CE平分∠B′CD,加上CA=CA′,所以根据等腰三角形的性质可得CE垂直平分AA′,则可对②进行判断;根据线段垂直平分线的性质得EA=EA′,则可对③进行判断;利用△DEA′和△B′EA都是等腰直角三角形,加上EA=EA′,可判断△DEA′≌△B′EA,于是可对④进行判断.
解答:解:∵正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),
∴∠B′A′C=45°,∠ADC=90°,CB=CB′,CA=CA′,
∴△A′DE为等腰直角三角形,
∴DA′=DE,
在△ADA′和△CDE中
,
∴△ADA′≌△CDE(SAS),所以①正确;
∵CB′=CB=CD,
而CE=CE,
∴Rt△CB′E≌Rt△CDE,
∴∠B′CE=∠DCE,
即CE平分∠B′CD,
∵CA=CA′,
∴CE垂直平分AA′,所以②正确;
∴EA=EA′,
∴△AEA′是等腰三角形,所以③正确;
∵△DEA′和△B′EA都是等腰直角三角形,
而EA=EA′,
∴△DEA′≌△B′EA,
∴S△DEA′=S△B′EA,所以④正确.
∴∠B′A′C=45°,∠ADC=90°,CB=CB′,CA=CA′,
∴△A′DE为等腰直角三角形,
∴DA′=DE,
在△ADA′和△CDE中
|
∴△ADA′≌△CDE(SAS),所以①正确;
∵CB′=CB=CD,
而CE=CE,
∴Rt△CB′E≌Rt△CDE,
∴∠B′CE=∠DCE,
即CE平分∠B′CD,
∵CA=CA′,
∴CE垂直平分AA′,所以②正确;
∴EA=EA′,
∴△AEA′是等腰三角形,所以③正确;
∵△DEA′和△B′EA都是等腰直角三角形,
而EA=EA′,
∴△DEA′≌△B′EA,
∴S△DEA′=S△B′EA,所以④正确.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了三角形全等的判定与性质和正方形的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在电视访谈节目中,一位气象专家说“本地区未来10天内发生降水的概率是三分之二”,以下哪个选项最能反映气象专家的意思( )
| A、这个地区从现在开始经过6至7天会发生降水 |
| B、这个地区未来10天内将会发生一次降水 |
| C、这个地区未来10天内发生降水比不发生降水的可能性大 |
| D、我们不能判断何时会有降水发生 |
若正方形的对角线长为8cm,则这个正方形的面积为( )
| A、32cm2 | ||
| B、64cm2 | ||
C、8
| ||
D、32
|
下列说法正确的是( )
| A、无限小数都是无理数 |
| B、无理数都是无限小数 |
| C、有理数只是有限小数 |
| D、实数可以分为正实数和负实数 |
 如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕为BC.
如图,将长方形纸片的一角折叠,使顶点A落在点A′处,折痕为BC.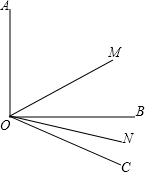 已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°
已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°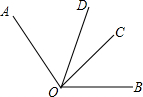 如图,已知:OD是∠AOB的平分线,∠AOC=2∠COB.
如图,已知:OD是∠AOB的平分线,∠AOC=2∠COB.