题目内容
点P的坐标恰好是(2x-1)(x+1)=0的两根,则P点在第( )象限.
分析:首先求出x的值,再利用点的坐标特点得出所在象限.
解答:解:∵点P的坐标恰好是(2x-1)(x+1)=0的两根,
∴2x-1=0或x+1=0,
解得:x1=
,x2=-1,
∴P点坐标为:(
,-1)或(-1,
),
∴则P点在第二、四象限.
故选:C.
∴2x-1=0或x+1=0,
解得:x1=
| 1 |
| 2 |
∴P点坐标为:(
| 1 |
| 2 |
| 1 |
| 2 |
∴则P点在第二、四象限.
故选:C.
点评:此题主要考查了因式分解一元二次方程和点的坐标确定位置,根据已知得出P点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
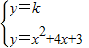 的两组解.若M在x轴上,△ABM可能是等腰三角形吗?若可能,求出点M的坐标;若不可能,说明理由.
的两组解.若M在x轴上,△ABM可能是等腰三角形吗?若可能,求出点M的坐标;若不可能,说明理由.