Question

如图1，在△OAB中，∠OAB＝90º，∠AOB＝30º，OB＝8．以OB为一边，在△OAB外作等边三角形OBC，D是OB的中点，连接AD并延长交OC于E．
【小题1】求点B的坐标
【小题2】求证：四边形ABCE是平行四边形；
【小题3】如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．

Answer 1

【小题1】∵在△OAB中，∠OAB＝90º，∠AOB＝30º，OB＝8，
∴OA＝4，AB＝4。∴点B的坐标为（4，4）。………2分
【小题2】∵∠OAB＝90º，∴AB⊥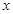轴，∴AB∥EC。 又∵△OBC是等边三角形，∴OC＝OB＝8。
又∵D是OB的中点，即AD是Rt△OAB斜边上的中线，
∴AD＝OD，∴∠OAD＝∠AOD＝30º，∴OE＝4。∴EC＝OC－OE＝4。
∴AB＝EC。∴四边形ABCE是平行四边形。……………………………………………………6分
【小题3】设OG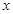＝，则由折叠对称的性质，得GA＝GC＝8－。
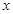在Rt△OAG中，由勾股定理，得，即，
解得，。∴OG的长为1。………………………………………………………………10分

解析