题目内容
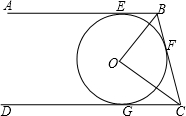 如图,BE、BC、CG分别切圆O于点E、F、G,且BE∥CG.
如图,BE、BC、CG分别切圆O于点E、F、G,且BE∥CG.(1)若BE=4,CG=9,求圆O的半径;
(2)若BO=6,CO=8,求圆O的半径.
考点:切线的性质
专题:
分析:如图,连接EG、OF.构建相似三角形,利用相似三角形的对应边成比例来求圆O的半径.
(1)通过△EBO∽△GOC的对应边成比例来求该圆的半径;
(2)勾股定理求得BC的长度,然后利用面积法来求OF的长度.
(1)通过△EBO∽△GOC的对应边成比例来求该圆的半径;
(2)勾股定理求得BC的长度,然后利用面积法来求OF的长度.
解答:解:如图,连接EG、OF.
(1)∵BE、BC分别切圆O于点E、F,
∴BE=BF.
∵在△BEO与△BFO中,
,
∴△BEO≌△BFO(SSS),
∴∠EBO=∠FBO.
同理,∠GCO=∠FCO.
∵BE∥CG.
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=
(∠ABC+∠DCB)=90°,
∠BOC=90°.
又BE、CG分别切圆O于点E、G,
∴点E、O、F三点共线,∠OEB=∠OGC=90°,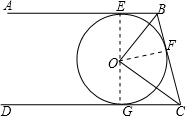
∴∠EOB=∠GCO,
∴△EBO∽△GOC,
∴
=
,即
=
,
则OG=6,即圆O的半径是6;
(2)由(1)知,∠BOC=90°.
∵BO=6,CO=8,
∴由勾股定理得到:BC=
=10.
∵BC是⊙O的切线,F是切点,
∴OF⊥BC,
∴
OB•OC=
BC•OF,则OF=
=
=4.8,即圆O的半径是4.8.
(1)∵BE、BC分别切圆O于点E、F,
∴BE=BF.
∵在△BEO与△BFO中,
|
∴△BEO≌△BFO(SSS),
∴∠EBO=∠FBO.
同理,∠GCO=∠FCO.
∵BE∥CG.
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=
| 1 |
| 2 |
∠BOC=90°.
又BE、CG分别切圆O于点E、G,
∴点E、O、F三点共线,∠OEB=∠OGC=90°,

∴∠EOB=∠GCO,
∴△EBO∽△GOC,
∴
| BE |
| OG |
| EO |
| GC |
| 4 |
| OG |
| OG |
| 9 |
则OG=6,即圆O的半径是6;
(2)由(1)知,∠BOC=90°.
∵BO=6,CO=8,
∴由勾股定理得到:BC=
| OB2+OC2 |
∵BC是⊙O的切线,F是切点,
∴OF⊥BC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| OB•OC |
| BC |
| 48 |
| 10 |
点评:本题考查了切线的性质、勾股定理以及相似三角形的判定与性质的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数
如图,数轴上有O,A,B,C,D五点,根据图中各点所表示的数,表示数| 18 |
| A、点O和A之间 |
| B、点A和B之间 |
| C、点B和C之间 |
| D、点C和D之间 |
 如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°. 如图所示,已知DO⊥CO,∠1=36°,∠3=36°.
如图所示,已知DO⊥CO,∠1=36°,∠3=36°.