题目内容
 (2013•盘锦)如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )
(2013•盘锦)如图,将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合.正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为s,则s关于t的函数图象为( )分析:分类讨论:当0≤t≤2时,BG=t,BE=2-t,运用△EBP∽△EGF的相似比可表示PB=1-
t,S为梯形PBGF的面积,则S=
(4-2t+4)•t=-t2+4t,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=
FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),∴S为三角形PAE的面积,则S=
(t-6)2,其图象为开口向上的抛物线的一部分.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:当0≤t≤2时,如图 ,
,
BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴
=
,即
=
,
∴PB=4-2t,
∴S=
(PB+FG)•GB=
(4-2t+4)•t=-t2+4t;
当2<t≤4时,S=
FG•GE=4;
当4<t≤6时,如图,
GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴
=
,即
=
,
∴PA=2(6-t),
∴S=
PA•AE=
•2(6-t)(6-t)
=
(t-6)2,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
 ,
,BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴
| PB |
| FG |
| EB |
| EG |
| PB |
| 4 |
| 2-t |
| 2 |
∴PB=4-2t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
当2<t≤4时,S=
| 1 |
| 2 |
当4<t≤6时,如图,

GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴
| PA |
| FG |
| EA |
| EG |
| PA |
| 4 |
| 6-t |
| 2 |
∴PA=2(6-t),
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
点评:本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.

练习册系列答案
相关题目

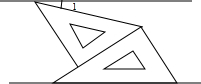 (2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
(2013•盘锦)如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( ) (2013•盘锦)如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )
(2013•盘锦)如图,△ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE为直径的圆与BC的位置关系是( )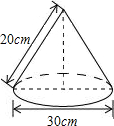 (2013•盘锦)如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是
(2013•盘锦)如图,张老师在上课前用硬纸做了一个无底的圆锥形教具,那么这个教具的用纸面积是