题目内容
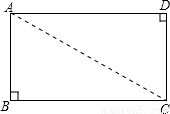
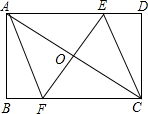 如图:矩形纸片ABCD中,AB=6cm,BC=8cm,将它沿EF折叠,使C与A重合,
如图:矩形纸片ABCD中,AB=6cm,BC=8cm,将它沿EF折叠,使C与A重合,
求:(1)折痕EF长;(2)若将折叠后的纸片放在桌面上,则纸片覆盖桌面的面积是多少?
解:(1)由题意得:AC=10,OC=5,且AC⊥EF,
∴△OFC∽△BAC,则 ,
,
∴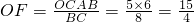 ,
,
又∵△AOE≌△COF,
∴OE=OF,EF=2OF= cm
cm
(2)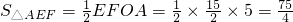 ,
,
∴覆盖桌面的面积是: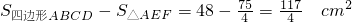 .
.
分析:(1)由勾股定理得,AC=10,OC=5,由AC⊥EF,得△OFC∽△BAC,则 ,再由△AOE≌△COF,可求得EF的长;
,再由△AOE≌△COF,可求得EF的长;
(2)先求△AEF的面积,再用四边形ABCD的面积减去△AEF的面积.
点评:本题考查了本题考查了矩形的性质、全等三角形的判定和性质、相似三角形的判定和性质、翻折变换等知识,综合性强,难度较大.
∴△OFC∽△BAC,则
 ,
,∴
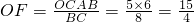 ,
,又∵△AOE≌△COF,
∴OE=OF,EF=2OF=
 cm
cm(2)
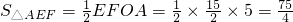 ,
,∴覆盖桌面的面积是:
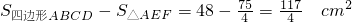 .
.分析:(1)由勾股定理得,AC=10,OC=5,由AC⊥EF,得△OFC∽△BAC,则
 ,再由△AOE≌△COF,可求得EF的长;
,再由△AOE≌△COF,可求得EF的长;(2)先求△AEF的面积,再用四边形ABCD的面积减去△AEF的面积.
点评:本题考查了本题考查了矩形的性质、全等三角形的判定和性质、相似三角形的判定和性质、翻折变换等知识,综合性强,难度较大.

练习册系列答案
相关题目
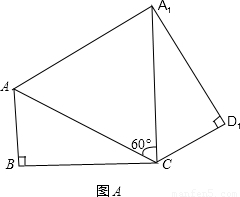
 如图,矩形纸片ABCD中,AB=4,BC=4
如图,矩形纸片ABCD中,AB=4,BC=4
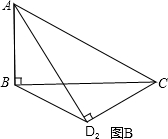

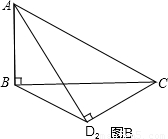
 把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E.
把△ABC、△ADC沿对角线AC翻折交AD、BC于点F、E. ,将矩形沿对角线AC剪开,解答以下问题:
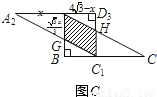
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.



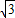 ,将矩形沿对角线AC剪开,解答以下问题:
,将矩形沿对角线AC剪开,解答以下问题: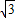 ),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.
),△A2C1D3是平移后的新位置(图C),若△ABC与△A2C1D3重叠部分的面积为y,求y关于x的函数关系式.