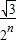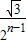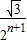题目内容
直线
与x、y轴交于B、A，点M为双曲线
上的一点，若△MAB为等边三角形，则k=-
-5或
．
【答案】分析：首先根据直线AB的解析式，求得A、B两点的坐标，即可得AB的长度，若△MAB是等边三角形，那么MA=MB=AB，可设出点M的坐标，然后利用坐标系两点间的距离公式，分别表示出MA、MB的长，将AB的值代入上述两式，通过联立方程组即可求得k的值．
解答：解：直线
中，y=0，则x=5；x=0，则y=-1；
故A（0，-1），B（5，0），AB2=26；
设点M（a，b），则：
MA2=a2+（b+1）2，MB2=（a-5）2+b2；
由△MAB是等边三角形可得到：
a2+（b+1）2=26，（a-5）2+b2=26，
解得：
或
；
∴k=ab=-
-5或
．
故答案为：=-
-5或
．
点评：本题考查了反比例函数的图象的性质以及等边三角形的性质，此题的思路并不复杂，难点在于复杂的计算过程，需要细心求解．
解答：解：直线
中，y=0，则x=5；x=0，则y=-1；故A（0，-1），B（5，0），AB2=26；
设点M（a，b），则：
MA2=a2+（b+1）2，MB2=（a-5）2+b2；
由△MAB是等边三角形可得到：
a2+（b+1）2=26，（a-5）2+b2=26，
解得：
或；∴k=ab=-
-5或．故答案为：=-
-5或．点评：本题考查了反比例函数的图象的性质以及等边三角形的性质，此题的思路并不复杂，难点在于复杂的计算过程，需要细心求解．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
与x，y轴交于点A，B，作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上，三角板的两边始终过点O，A，并且不断地转动三角板.
时，求经过A，O，C三点的抛物线的解析式，直接写出顶点坐标；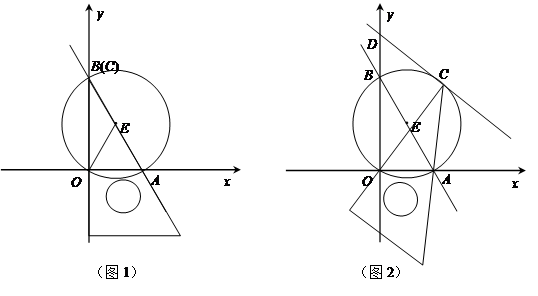
与x、y轴交于B、A，点M为双曲线
上的一点，若△MAB为等边三角形，则k=-
-5或
．
与x，y轴交于点A，B，作△AOB为外接⊙E.将直角三角板的30°角的顶点C摆放在圆弧上，三角板的两边始终过点O，A，并且不断地转动三角板.
时，求经过A，O，C三点的抛物线的解析式，直接写出顶点坐标；
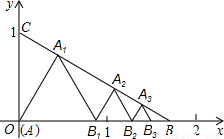
与x、y轴交于B、C两点，A（0，0），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第n个等边三角形的边长等于（ ）
