题目内容
已知点 在直线
在直线 上,若
上,若 ,
, 试比较
试比较 和
和 的大小,并说明理由.
的大小,并说明理由.
【答案】
n2<n1.理由见解析.
【解析】
试题分析:根据A(m1,n1),B(m2,n2)在直线y=kx+b上,,可得出n1,n2的值,再得出n1+n2=k(m1+m2)+2b,故可得出k+1= ,再根据b>2可知0<
,再根据b>2可知0< <1,故可得出0<k+1<1,再由m1<m2即可得出结论.
<1,故可得出0<k+1<1,再由m1<m2即可得出结论.
试题解析:∵A(m1,n1),B(m2,n2)在直线y=kx+b上,
∴n1=km1+b,n2=km2+b.
∴n1+n2=k(m1+m2)+2b.
∴kb+4=3kb+2b.
∴k+1= .
.
∵b>2,
∴0< <1.
<1.
∴0<k+1<1.
∴-1<k<0.
∵m1<m2,
∴n2<n1.
考点:一次函数图象上点的坐标.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 ,点
,点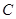 在直线
在直线 上,若
上,若 ,且
,且 为
为 cm.
cm.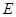 在直线
在直线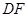 上,点
上,点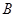 在直线
在直线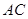 上,若
上,若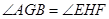 .
.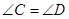 ,则
,则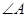 与
与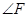 相等吗?为什么?
相等吗?为什么? ,点
,点 在直线
在直线 上,若
上,若 ,且
,且 为
为 cm.
cm.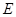 在直线
在直线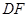 上,点
上,点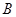 在直线
在直线 上,若
上,若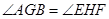 .
.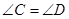 ,则
,则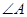 与
与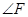 相等吗?为什么?
相等吗?为什么?