题目内容
 如图:AD为△ABC的高,∠B=2∠C,DC=3BD,若AD=3,求AC的长.
如图:AD为△ABC的高,∠B=2∠C,DC=3BD,若AD=3,求AC的长.
解:
在DC上截取DE=BD,连接AE,
∵CD=3BD,
∴CE=2BD=2DE,
∵BD=DE,AD⊥BE,
∴AB=AE,
∴∠B=∠AEB,
∵∠B=2∠C,
∴∠AEB=2∠C,
∵∠AEB=∠C+∠EAC,
∴∠EAC=∠C,
∴AE=CE=2DE=2BD=BE,
设DE=a,则AE=CE=BE=2a,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
∴32+a2=(2a)2,
a= ,
,
∴DE= ,CD=3
,CD=3 ,
,
在Rt△ADC中,由勾股定理得:AC=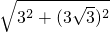 =6.
=6.
分析:在DC上截取DE=BD,连接AE,求出AB=AE,求出∠B=∠AEB,根据∠B=2∠C和∠AEB=∠C+∠EAC求出∠EAC=∠C,推出AE=CE=2DE=2BD=BE,设DE=a,则AE=CE=BE=2a,在Rt△ADE中,由勾股定理得出AD2+DE2=AE2,求出a= ,得出DE=
,得出DE= ,CD=3
,CD=3 ,在Rt△ADC中,由勾股定理求出AC即可.
,在Rt△ADC中,由勾股定理求出AC即可.
点评:本题考查了等腰三角形的性质和判定,线段的垂直平分线,勾股定理,三角形的外角性质等知识点的综合运用,题目综合性比较强,有一定的难度.

在DC上截取DE=BD,连接AE,
∵CD=3BD,
∴CE=2BD=2DE,
∵BD=DE,AD⊥BE,
∴AB=AE,
∴∠B=∠AEB,
∵∠B=2∠C,
∴∠AEB=2∠C,
∵∠AEB=∠C+∠EAC,
∴∠EAC=∠C,
∴AE=CE=2DE=2BD=BE,
设DE=a,则AE=CE=BE=2a,
在Rt△ADE中,由勾股定理得:AD2+DE2=AE2,
∴32+a2=(2a)2,
a=
 ,
,∴DE=
 ,CD=3
,CD=3 ,
,在Rt△ADC中,由勾股定理得:AC=
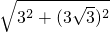 =6.
=6.分析:在DC上截取DE=BD,连接AE,求出AB=AE,求出∠B=∠AEB,根据∠B=2∠C和∠AEB=∠C+∠EAC求出∠EAC=∠C,推出AE=CE=2DE=2BD=BE,设DE=a,则AE=CE=BE=2a,在Rt△ADE中,由勾股定理得出AD2+DE2=AE2,求出a=
 ,得出DE=
,得出DE= ,CD=3
,CD=3 ,在Rt△ADC中,由勾股定理求出AC即可.
,在Rt△ADC中,由勾股定理求出AC即可.点评:本题考查了等腰三角形的性质和判定,线段的垂直平分线,勾股定理,三角形的外角性质等知识点的综合运用,题目综合性比较强,有一定的难度.

练习册系列答案
相关题目
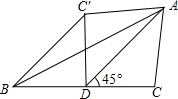 如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.
如图,AD为△ABC的中线,∠ADC=45°,把△ADC沿AD对折,点C落在点C′的位置,BC=4,求BC′的长.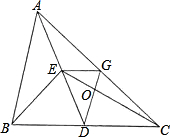 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为三角形ABD中线,
如图,AD为△ABC的中线,BE为三角形ABD中线, 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线. 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.