题目内容
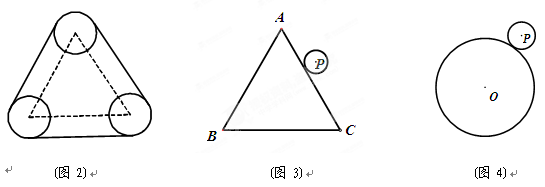
 如图△ABC的两个外角的平分线交于点D,若∠B=60°,则∠D等于( )
如图△ABC的两个外角的平分线交于点D,若∠B=60°,则∠D等于( )| A、60° | B、80° | C、65° | D、30° |
分析:先求出∠BAC+∠BCA的度数,然后根据平角求出∠EAC+∠ACF的度数,根据AD、CD分别是外角平分线,即可求出∠CAD+∠ACD的度数,最后在△ACD中,利用三角形内角和等于180°即可求出∠D.
解答:解:∵∠B=60°,
∴∠BAC+∠BCA=180°-60°=120°,
∴∠EAC+∠ACF=360°-120°=240°,
∵AD、CD是外角平分线,
∴∠CAD+∠ACD=
(∠EAC+∠ACF)=
×240°=120°,
在△ACD中,∠D=180°-(∠CAD+∠ACD)=180°-120°=60°.
故选A.
∴∠BAC+∠BCA=180°-60°=120°,
∴∠EAC+∠ACF=360°-120°=240°,
∵AD、CD是外角平分线,
∴∠CAD+∠ACD=
| 1 |
| 2 |
| 1 |
| 2 |
在△ACD中,∠D=180°-(∠CAD+∠ACD)=180°-120°=60°.
故选A.
点评:本题主要考查了三角形内角和定理,整体思想的利用对解本题比较关键.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 (2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.
(2012•潍坊)如图,三角形ABC的两个顶点B、C在圆上,顶点A在圆外,AB、AC分别交圆于E、D两点,连接EC、BD.