题目内容
已知正方形ABCD的边长是4，点E在直线AD上，DE=2，连接BE与对角线AC相交于点F，则CF：FA的值是分析：因为点E的位置有两种情况：E在线段AD上和在AD的延长线上．然后分别求解．
解答：解：如图，点E的位置有两种情况：
①当E点在线段AD上，如图，
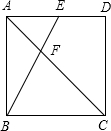
∵AE=AD-DE=2，AE∥BC，
∴CF：FA=BC：AE=4：2=2，
②当点E在线段AD的延长线上时，如图，
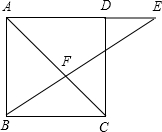
∵DE=2，AE=6，
∵AE∥BC，
∴CF：FA=BC：AE=4：6=
．
∴由①②可知：CF：FA的值是2或
．
①当E点在线段AD上，如图，
∵AE=AD-DE=2，AE∥BC，
∴CF：FA=BC：AE=4：2=2，
②当点E在线段AD的延长线上时，如图，
∵DE=2，AE=6，
∵AE∥BC，
∴CF：FA=BC：AE=4：6=
| 2 |
| 3 |
∴由①②可知：CF：FA的值是2或
| 2 |
| 3 |
点评：本题利用了正方形的性质和平行线分对应线段成比例的性质，注意有两种情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
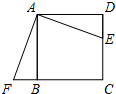如图，已知正方形ABCD的边长为12cm，E为CD边上一点，DE=5cm．以点A为中心，将△ADE按顺时针方向旋转得△ABF，则点E所经过的路径长为
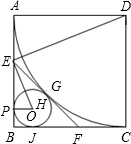合），过点E作弧AC的切线，交BC于点F，G为切点，⊙O是△EBF的内切圆，分别切EB、BF、FE于点P、J、H
（2011•同安区质检）如图，已知正方形ABCD的边长是2，E是AB的中点，延长BC到点F使CF=AE．
（2012•香洲区一模）如图，已知正方形ABCD的边长为28，动点P从A开始在线段AD上以每秒3个单位长度的速度向点D运动（点P到达点D时终止运动），动直线EF从AD开始以每秒1个单位长度的速度向下平行移动（即EF∥AD），并且分别与DC、AC交于E、F两点，连接FP，设动点P与动直线EF同时出发，运动时间为t 秒．
如图，已知正方形ABCD的边长为8cm，点E、F分别在边BC、CD上，∠EAF=45°．当EF=8cm时，△AEF的面积是