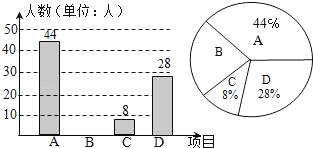
题目内容
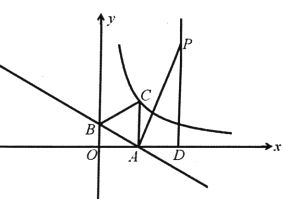
【题目】如图,已知等腰直角△ABC中,∠BAC=90°,AD⊥BC于点D,AB=5,点E是边AB上的动点(不与A,B点重合),连接DE,过点D作DF⊥DE交AC于点F,连接EF,点H在线段AD上,且DH=![]() AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.
AD,连接EH,HF,记图中阴影部分的面积为S1,△EHF的面积记为S2,则S2的取值范围是_______.

【答案】![]() ≤S2<
≤S2<![]()
【解析】
作EM⊥BC于M,作FN⊥AD于N,根据题意可证△ADF≌△BED,可得△DFE是等腰直角三角形.可证△BME≌△ANF,可得NF=BM.所以S1=![]() HD×BD,代入可求S1,由点E是边AB上的动点(不与A,B点重合),可得DE垂直AB时DE最小,即
HD×BD,代入可求S1,由点E是边AB上的动点(不与A,B点重合),可得DE垂直AB时DE最小,即![]() ≤DE<
≤DE<![]() ,且S2=S△DEF-S1,代入可求S2的取值范围
,且S2=S△DEF-S1,代入可求S2的取值范围
解:作EM⊥BC于M,作FN⊥AD于N,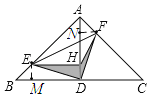
∵EM⊥BD,AD⊥BC
∴EM∥AD
∵△ABC是等腰直角三角形,AD⊥BC,AB=5
∴∠B=∠C=45°=∠BAD=∠DAC,BD=CD=AD=![]()
∵DF⊥DE
∴∠ADF+∠ADE=90°且∠ADE+∠BDE=90°
∴∠ADF=∠BDE且AD=BD,∠B=∠DAF=45°
∴△ADF≌△BDE,
∴AF=BE,DE=DF
∴△DEF是等腰直角三角形,
∵AF=BE,∠B=∠DAF=45°,∠EMB=∠ANF=90°
∴△BME≌△ANF
∴NF=BM
∵S1=S△EHD+S△DHF=![]() HD×MD+
HD×MD+![]() HD×FN=
HD×FN=![]() ×
×![]() AD×(BM+MD)=
AD×(BM+MD)=![]() AD2=
AD2=![]()
∵点E是边AB上的动点
∴![]() ≤DE<
≤DE<![]() ,
,
∵S2=S△DEF-S1=![]() DE2-
DE2-![]()
∴![]() ≤S2<
≤S2<![]()
故答案为:![]() ≤S2<
≤S2<![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目