题目内容
 长方形ABCD中,已知AB=8,AO=5,则矩形ABCD的面积为________.
长方形ABCD中,已知AB=8,AO=5,则矩形ABCD的面积为________.
48
分析:根据AO即可求AC的长,在Rt△ABC中,已知AB,AC根据勾股定理即可求得BC的长,根据AB,BC的值即可求得矩形ABCD的面积.
解答:∵AO=5∴AC=10,
在直角△ABC中,
已知AB=8、AC=10,
∴BC= =6,
=6,
∴矩形ABCD的面积为6×8=48,
故答案为 48.
点评:本题考查了矩形面积的计算,考查了勾股定理在直角三角形中的运用,考查了矩形对角线互相平分的性质,本题中根据勾股定理求BC的面积是解题的关键.
分析:根据AO即可求AC的长,在Rt△ABC中,已知AB,AC根据勾股定理即可求得BC的长,根据AB,BC的值即可求得矩形ABCD的面积.
解答:∵AO=5∴AC=10,
在直角△ABC中,
已知AB=8、AC=10,
∴BC=
 =6,
=6,∴矩形ABCD的面积为6×8=48,
故答案为 48.
点评:本题考查了矩形面积的计算,考查了勾股定理在直角三角形中的运用,考查了矩形对角线互相平分的性质,本题中根据勾股定理求BC的面积是解题的关键.

练习册系列答案
相关题目
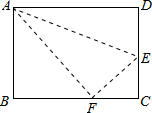 如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=
如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=
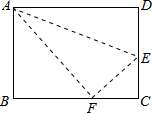 如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=________cm.
如图,长方形ABCD中,已知AB=8cm,BC=10cm,将AD沿直线AF折叠,使得点D落在BC边上的点E处,则CF=________cm.