题目内容
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥DC,BC=10cm,CD=6cm.在线段BC、CD上有动点F、E,点F以每秒2cm的速度,在线段BC上从点B向点C匀速运动;同时点E以每秒1cm的速度,在线段CD上从点C向点D匀速运动.当点F到达点C时,点E同时停止运动.设点F运动的时间为t(秒).
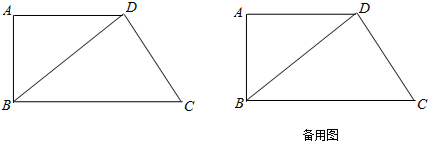
(1)求AD的长;
(2)设四边形BFED的面积为y,求y 关于t的函数关系式,并写出函数自变量取值范围;
(3)点F、E在运动过程中,如△CEF与△BDC相似,求线段BF的长.
(4)以BF为半径的圆B与以DE为半径的圆D如果相切,直接写出t的值.
解:(1)在Rt△BCD中,CD=6cm,BC=10cm,
所以BD=8cm.
因为AD∥BC,所以∠ADB=∠CBD.
在Rt△BCD中,BD=8cm,cos∠ADB=cos∠CBD= =
= ,
,
所以AD=BDcos∠ADB=8× =
= (cm).
(cm).
(2)如图2,过点E作EH⊥AB,垂足为H.
在Rt△CEH中,CE=t,sin∠C= ,
,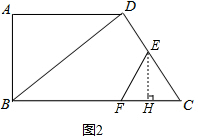
所以EH=CE sin∠C= t.
t.
∵△BCD的面积为24,
∴S△CEF= CF•EH=
CF•EH= (10-2t)×
(10-2t)× t=-
t=- t2+4t,
t2+4t,
所以y=S△BCD-S△CEF=24-(- t2+4t)=
t2+4t)= t2-4t+24(0<t<5);
t2-4t+24(0<t<5);
(3)①如图3,当∠CEF=90°时,
∵BD⊥CD,
∴BD∥EF,
∴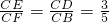 .
.
∴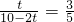 .
.
解得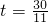 .
.
此时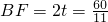 (cm).
(cm).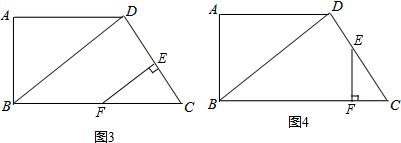
②如图4,当∠CFE=90°时,
∵∠C=∠C,∠BDC=∠EFC,
∴△EFC∽△BDC,
∴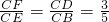 .
.
所以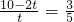 .
.
解得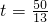 .此时
.此时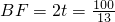 (cm).
(cm).
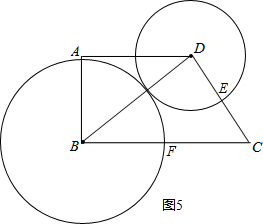 (4)如图5,当以BF为半径的圆B与以DE为半径的圆D相外切,
(4)如图5,当以BF为半径的圆B与以DE为半径的圆D相外切,
DE=DC-EC=6-t,BF=2t,
则BD=BF+DE=2t+6-t=8,
解得:t=2(秒).
当以BF为半径的圆B与以DE为半径的圆D相内切,
DE=DC-EC=6-t,BF=2t,
则BD=BF-DE=2t-(6-t)=8,
解得:t= (秒).
(秒).
故当t的值为2秒与 秒时,以BF为半径的圆B与以DE为半径的圆D相切.
秒时,以BF为半径的圆B与以DE为半径的圆D相切.
分析:(1)利用勾股定理求出BD的长,再利用cos∠ADB=cos∠CBD= 进而求出AD的长即可;
进而求出AD的长即可;
(2)首先用t表示出EH的长以及FC的长,进而利用y=S△BCD-S△CEF得出函数关系即可;
(3)分别利用①如图3,当∠CEF=90°时,②如图4,当∠CFE=90°时,利用相似三角形的性质求出即可;
(4)分别利用当两圆相外切或内切,利用外切时圆心距=r+R,内切时圆心距=R-r,得出答案即可.
点评:此题主要考查了相且两圆的性质以及相似三角形的判定与性质以及锐角三角函数等知识,根据已知画出图象进行分类讨论得出是解题关键.
所以BD=8cm.
因为AD∥BC,所以∠ADB=∠CBD.
在Rt△BCD中,BD=8cm,cos∠ADB=cos∠CBD=
 =
= ,
,所以AD=BDcos∠ADB=8×
 =
= (cm).
(cm).(2)如图2,过点E作EH⊥AB,垂足为H.
在Rt△CEH中,CE=t,sin∠C=
 ,
,
所以EH=CE sin∠C=
 t.
t.∵△BCD的面积为24,
∴S△CEF=
 CF•EH=
CF•EH= (10-2t)×
(10-2t)× t=-
t=- t2+4t,
t2+4t,所以y=S△BCD-S△CEF=24-(-
 t2+4t)=
t2+4t)= t2-4t+24(0<t<5);
t2-4t+24(0<t<5);(3)①如图3,当∠CEF=90°时,
∵BD⊥CD,
∴BD∥EF,
∴
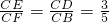 .
.∴
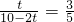 .
.解得
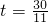 .
.此时
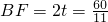 (cm).
(cm).
②如图4,当∠CFE=90°时,
∵∠C=∠C,∠BDC=∠EFC,
∴△EFC∽△BDC,
∴
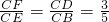 .
.所以
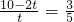 .
.解得
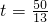 .此时
.此时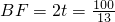 (cm).
(cm). (4)如图5,当以BF为半径的圆B与以DE为半径的圆D相外切,
(4)如图5,当以BF为半径的圆B与以DE为半径的圆D相外切,DE=DC-EC=6-t,BF=2t,
则BD=BF+DE=2t+6-t=8,
解得:t=2(秒).
当以BF为半径的圆B与以DE为半径的圆D相内切,
DE=DC-EC=6-t,BF=2t,
则BD=BF-DE=2t-(6-t)=8,
解得:t=
 (秒).
(秒).故当t的值为2秒与
 秒时,以BF为半径的圆B与以DE为半径的圆D相切.
秒时,以BF为半径的圆B与以DE为半径的圆D相切.分析:(1)利用勾股定理求出BD的长,再利用cos∠ADB=cos∠CBD=
 进而求出AD的长即可;
进而求出AD的长即可;(2)首先用t表示出EH的长以及FC的长,进而利用y=S△BCD-S△CEF得出函数关系即可;
(3)分别利用①如图3,当∠CEF=90°时,②如图4,当∠CFE=90°时,利用相似三角形的性质求出即可;
(4)分别利用当两圆相外切或内切,利用外切时圆心距=r+R,内切时圆心距=R-r,得出答案即可.
点评:此题主要考查了相且两圆的性质以及相似三角形的判定与性质以及锐角三角函数等知识,根据已知画出图象进行分类讨论得出是解题关键.

练习册系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.