题目内容
计算
(1)
(2)
(3)当x=2时,求 的值.
的值.
解:(1)原式= •
• =-
=- •
• =-1;
=-1;
(2)原式= ÷(
÷( ÷
÷ )=
)= ÷(
÷( ×
× )=
)= ×
× =
= =-1;
=-1;
(3)原式= ÷
÷ =
= ×
× =
= ,
,
当x=2时,原式=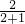 =
= .
.
分析:(1)先按照负整数指数幂的定义把分子、分母化简,化为最简后再算乘法即可;
(2)先算括号内的除法,化为最简后再算括号外的除法;
(3)先把括号内的分式通分并化简,然还算除法,化为最简后再把x的值代入即可.
点评:本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.此题比较简单,但计算时要细心才行.
 •
• =-
=- •
• =-1;
=-1;(2)原式=
 ÷(
÷( ÷
÷ )=
)= ÷(
÷( ×
× )=
)= ×
× =
= =-1;
=-1;(3)原式=
 ÷
÷ =
= ×
× =
= ,
,当x=2时,原式=
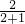 =
= .
.分析:(1)先按照负整数指数幂的定义把分子、分母化简,化为最简后再算乘法即可;
(2)先算括号内的除法,化为最简后再算括号外的除法;
(3)先把括号内的分式通分并化简,然还算除法,化为最简后再把x的值代入即可.
点评:本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.此题比较简单,但计算时要细心才行.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
