题目内容
 如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是________.
如图,l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,面积是25的正方形ABCD的四个顶点分别在这四条直线上,那么h的值是________.

分析:根据平行线的性质可设AE=x,则AD=2x,由勾股定理得出BE=
 x,再根据三角形的面积公式求得正方形ABCD的边长,从而求得正方形ABCD的面积,再根据面积为25可求出h的值.
x,再根据三角形的面积公式求得正方形ABCD的边长,从而求得正方形ABCD的面积,再根据面积为25可求出h的值.解答:∵l1、l2、l3、l4是同一平面内的四条平行直线,且每相邻的两条平行直线间的距离为h,
∴设AE=x,则AD=2x,BE=
 x,
x,S△ABE=
 x•2x=
x•2x= •
• x•h,
x•h,
解得x=
 h,
h,AD=2x=
 h,
h,∴S正方形ABCD=5h2,
∵正方形ABCD面积是25,
∴5h2=25,
∴h=
 ,
,故答案为:
 .
.点评:本题考查了正方形的性质、平行线的性质、勾股定理等知识,根据三角形的面积公式得到正方形ABCD的边长是解决本题的关键.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )
22、某校八年级同学到距学校6千米的郊外春游,一部分同学步行,另一部分同学骑自行车,如图,l1、l2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数图象,则以下判断错误的是( )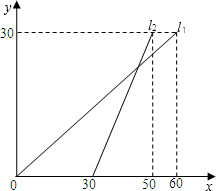 的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
的路程y(千米)随时间x(分钟)变化的函数图象.根据图象,解答下列问题:
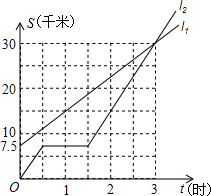 如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系.
如图,l1、l2分别表示步行者与骑自行车在同一路上行驶的路程S与时间t的关系. 如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)
如图,l1,l2分别表示一种白炽灯和一种节能灯的费用y与照明时间x(h)的函数图象,假设两种灯的使用寿命都是2000h,照明效果一样.(费用=灯的售价+电费,单位:元)