Question

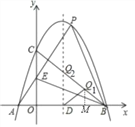
【题目】如图，已知抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，4）．

（1）求此抛物线的解析式；

（2）设点P（2，n）在此抛物线上，AP交y轴于点E，连接BE，BP，请判断△BEP的形状，并说明理由；

（3）设抛物线的对称轴交x轴于点D，在线段BC上是否存在点Q，使得△DBQ成为等腰直角三角形？若存在，求出点Q的坐标；若不存在，说明理由．

Answer 1

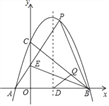
【答案】(1)y=﹣x2+3x+4；（2）△BEP为等腰直角三角形，理由见解析；（3）存在，Q的坐标为或.

【解析】试题分析：（1）待定系数法求二次函数解析式.(2)先求出直线AP解析式，分别求出BE,EP,BP的长度，由勾股定理逆定理△BEP的形状.(3)先求出二次函数的顶点，分类讨论，若BQ=DQ，BQ1⊥DQ1，∠BDQ=45°，过点Q1作Q1M⊥OB，垂足为M，可求得△DBQ是等腰三角形，可以得到Q点，若DQ2=BD，DQ2⊥BD，可以计算出Q点.

试题解析：

解：（1）∵抛物线上A、B、C三点坐标代入抛物线解析式y=ax2+bx+c

得，,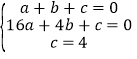

解得,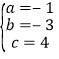

∴抛物线的解析式为y=﹣x2+3x+4．

（2）结论：△BEP为等腰直角三角形，理由如下：

∵点P（2，n）在此抛物线上，

∴n=﹣4+6+4=6，

∴P点坐标为（2，6）．

设直线AP解析式为y=kx+b，

把A、P两点坐标代入可得,

解得,

∴直线AP的解析式为y=2x+2，

令x=0可得y=2，则E点坐标为（0，2）．

∵B（4，0），P（2，6），

∴BP=2，BE=2，EP=2

∴BE2+EP2=20+20=40=BP2，且BE=EP，

∴△BEP为等腰直角三角形．

（3）存在．

∵y=﹣x2+3x+4=﹣（x﹣）2+,

∴顶点的坐标为（，），

∵OB=OC=4，∴BC=4，∠ABC=45°．

以下分两种情况：

①若BQ=DQ，BQ1⊥DQ1，∠BDQ=45°，如图，过点Q1作Q1M⊥OB，垂足为M，

∵BQ1=DQ1，BD=4﹣=，

∴BM=Q1M=，OM=4﹣=，

∴Q1的坐标为Q1（，）．

②若DQ2=BD=，DQ2⊥BD，易得BC所在的直线解析式为y=﹣x+4，

代入x=，得y=﹣+4=，

∴DQ2=BD=，∴△BDQ2是等腰直角三角形，

所以Q2的坐标为Q2（，），

综上所述，Q的坐标为Q1（，）或Q2（，）．