题目内容

【题目】已知：如图，二次函数y=ax2+bx+c的图象与x轴交于A、B两点，其中A点坐标为（﹣1，0），点C（0，5），另抛物线经过点（1，8），M为它的顶点．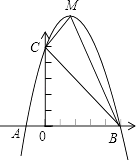

（1）求抛物线的解析式；
（2）求△MCB的面积S△MCB ．

【答案】
（1）解：依题意： ，

解得

∴抛物线的解析式为y=﹣x2+4x+5


（2）解：令y=0，得（x﹣5）（x+1）=0，x1=5，x2=﹣1，

∴B（5，0）．

由y=﹣x2+4x+5=﹣（x﹣2）2+9，得M（2，9）

作ME⊥y轴于点E，

可得S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC= （2+5）×9﹣ ×4×2﹣ ×5×5=15．


【解析】（1）把三个点的坐标代入，用待定系数法求出抛物线的解析；（2）根据抛物线的解析求出顶点M的坐标，求出S△MCB=S梯形MEOB﹣S△MCE﹣S△OBC的值.

练习册系列答案
相关题目

【题目】如图，在直角坐标系中，△ABC的三个顶点都在坐标轴上，A，B两点关于y轴对称，点C是y轴正半轴上一个动点，AD是角平分线．

（1）如图1，若∠ACB＝90°，直接写出线段AB，CD，AC之间数量关系；

（2）如图2，若AB＝AC+BD，求∠ACB的度数；

（3）如图2，若∠ACB＝100°，求证：AB＝AD+CD．

【题目】穿越青海境内的兰新高速铁路正在加紧施工．某工程队承包了一段全长1957米的隧道工程，甲、乙两个班组分别从南北两端同时掘进，已知甲组比乙组每天多掘进0.5米，经过6天施工，甲、乙两组共掘进57米．

（1）求甲乙两班组平均每天各掘进多少米？

（2）为加快工程进度，通过改进施工技术，在剩余的工程中，甲组平均每天比原来多掘进0.3米，乙组平均每天比原来多掘进0.2米．按此施工进度，能够比原来少用多少天完成任务？

【题目】如图，在 Rt△ABC中，∠ABC=90°，AB=CB，以AB为直径的⊙O交AC于点D，点E是AB边上一点（点E不与点A、B重合），DE的延长线交⊙O于点G，DF⊥DG，且交BC于点F．

（1）求证：AE=BF．
（2）连接GB，EF，求证：GB∥EF．
（3）若AE=1，EB=3，求DG的长．

【题目】如图，AB是⊙O的直径，弦CD⊥AB于点E，∠CDB=30°，CD=2 ，则阴影部分的面积为 ．

【题目】如图，折线ABCDE描述了一辆汽车在某一直线上行驶过程中，汽车离出发地的距离y(km)和行驶时间x(h)之间的函数关系，根据图中提供的信息，给出下列说法：①汽车共行驶了120km；②汽车在行驶途中停留了0.5h；③汽车在整个行驶过程中的平均速度为km/h；④汽车自出发后3h～4.5h之间行驶的速度在逐渐减小．其中正确的说法是 .（填上所有正确的序号）

【题目】小颖和小亮上山游玩，小颖乘坐缆车，小亮步行，两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍，小颖在小亮出发后50分才乘上缆车，缆车的平均速度为180米/分，设小亮出发x分后行走的路程为y米．图中的折线表示小亮在整个行走过程中y随x的变化关系.

（1)小亮行走的总路程是_________米，他途中休息了___________分；

（2）分别求出小亮在休息前和休息后所走的路程段上的步行速度；

（3）当小颖到达缆车终点时，小亮离缆车终点的路程是多少？

【题目】如图，在平面直角坐标系中，A(1，2)、B(3，1)、C(﹣2，﹣1)

(1)在图中作出△ABC关于y轴对称的△A1B1C1；

(2)写出A1、B1、C1的坐标；

(3)求△A1B1C1的面积．

【题目】如图，△ABC是等边三角形，BD平分∠ABC，延长BC到E，使得CE＝CD．

求证：BD＝DE．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网