题目内容
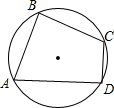如图，在圆内接四边形ABCD中，∠A=60°，∠B=90°，AB=2，CD=1，则BC=分析：连接AC，则AC是直径，得∠D=90°，延长BC、AD交于点E．在直角三角形ABE中，∠E=30°，AB=2，则BE=2
；在直角三角形CDE中，可以求得CE=2，从而确定BC的长．
| 3 |
解答：
解：连接AC，延长BC、AD交于点E．
∵∠B=90°，
∴AC是直径，
∴∠ADC=90°．
又∵∠BAD=60°，
∴∠E=30°，
∵CD=1，
∴BE=2
，CE=2，
∴BC=2
-2．
故答案为2
-2．
解：连接AC，延长BC、AD交于点E．∵∠B=90°，
∴AC是直径，
∴∠ADC=90°．
又∵∠BAD=60°，
∴∠E=30°，
∵CD=1，
∴BE=2
| 3 |
∴BC=2
| 3 |
故答案为2
| 3 |
点评：此题综合运用了圆周角定理的推论、解直角三角形的知识．
练习册系列答案
相关题目
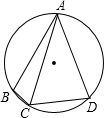如图，在圆内接四边形ABCD中，AB=AD，∠BAD=60°，AC=a，则四边形ABCD的面积为
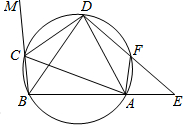延长DF与BA的延长线交于E．
16、已知如图，在圆内接四边形ABCD中，∠B=30°，则∠D=
如图：在圆内接四边形ABCD中，AB=AD，AC=1，∠ACD=60°，则四边ABCD的面积为（ ）| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|