题目内容
1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,根据前面各式的规律可猜测:1+3+5+7+…+(2n-1)=________(其中n是正整数).
n2
分析:从数字中找到规律,从小范围到大范围.
解答:从1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,三个等式中,可以看出等式左边最后一个数+1再除以2即得到等式右边幂的底数,
2=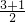 ,3=
,3=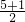 ,4=
,4= ,从而得
,从而得 =n,
=n,
即:1+3+5+7+…+(2n-1)=n2.
故答案为:n2.
点评:此题考查的知识点是数字的变化类问题,关键是明确从整体和局部分别找到规律.
分析:从数字中找到规律,从小范围到大范围.
解答:从1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,三个等式中,可以看出等式左边最后一个数+1再除以2即得到等式右边幂的底数,
2=
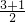 ,3=
,3=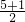 ,4=
,4= ,从而得
,从而得 =n,
=n,即:1+3+5+7+…+(2n-1)=n2.
故答案为:n2.
点评:此题考查的知识点是数字的变化类问题,关键是明确从整体和局部分别找到规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有理数-22,(-2)3,-|-2|,-(-
)中,负数有( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 9、某班全体同学在“献爱心”活动中都捐了图书,捐书的情况如下表:
9、某班全体同学在“献爱心”活动中都捐了图书,捐书的情况如下表: