题目内容
先化简,再求值:
(1)-2(x2+1)+5(x-5)- (4x2-2x),其中x=-1
(4x2-2x),其中x=-1 ;
;
(2)已知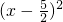 +|y+
+|y+ |=0,求x2-2y2-(-3xy+x2)-3(-y2+
|=0,求x2-2y2-(-3xy+x2)-3(-y2+ xy)的值.
xy)的值.
解:(1)原式=-2x2-2+5x-25-2x2+x=(-2x2-2x2)+(5x+x)+(-25-2)=-4x2+6x-27,
将x=-1 代入上式得,
代入上式得,
原式=-4× +6×(-1
+6×(-1 )-27=-45;
)-27=-45;
(2)由题意x= ,y=-
,y=- ,
,
∴原式=x2-2y2+3xy-x2+3y2- xy
xy
=(x2-x2)+(-2y2+3y2)+(3xy- xy)
xy)
=y2+ xy=
xy= +
+ ×
× ×(-
×(- )
)
= -
-
=- .
.
分析:(1)去括号,合并同类项,再代入求值;
(2)由非负数的性质求得x,y的值,把代数式去括号,合并同类项,再代入求值.
点评:(1)解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则;
(2)非负数的性质:若两个非负数的和为0,则这两个数均为0.
将x=-1
 代入上式得,
代入上式得,原式=-4×
 +6×(-1
+6×(-1 )-27=-45;
)-27=-45;(2)由题意x=
 ,y=-
,y=- ,
,∴原式=x2-2y2+3xy-x2+3y2-
 xy
xy=(x2-x2)+(-2y2+3y2)+(3xy-
 xy)
xy)=y2+
 xy=
xy= +
+ ×
× ×(-
×(- )
)=
 -
-
=-
 .
.分析:(1)去括号,合并同类项,再代入求值;
(2)由非负数的性质求得x,y的值,把代数式去括号,合并同类项,再代入求值.
点评:(1)解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则;
(2)非负数的性质:若两个非负数的和为0,则这两个数均为0.

练习册系列答案
相关题目